
| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | b>c>a |
分析 根据指数函数与幂函数的图象与性质,对a,b,c的大小关系进行比较即可.
解答 解:函数y=${(\frac{2}{3})}^{x}$是定义域R上的单调递减函数,且$\frac{1}{3}$<$\frac{2}{3}$,
∴${(\frac{2}{3})}^{\frac{1}{3}}$>${(\frac{2}{3})}^{\frac{2}{3}}$,即a>c;
又函数y=${x}^{\frac{2}{3}}$是(0,+∞)上的单调增函数,且$\frac{2}{3}$>$\frac{1}{3}$,
∴${(\frac{2}{3})}^{\frac{2}{3}}$>${(\frac{1}{3})}^{\frac{2}{3}}$,即c>b;
∴a,b,c的大小关系是a>c>b.
故选:B.
点评 本题考查了指数函数与对数函数的单调性,也考查了推理能力与计算能力,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{25}{2}$ | C. | 25 | D. | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
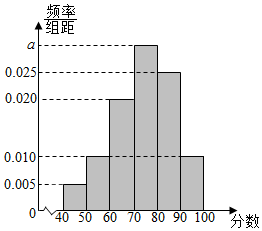 某校从高二年级学生中随机抽取40名学生,将他们的期中考试政治成绩(满分100分,成绩均不低于40分的整数)分成六段:[40,50),[50,60),[60,70),[70,80)[80,90),[90,100]后,得到如图所示的频率分布直方图.
某校从高二年级学生中随机抽取40名学生,将他们的期中考试政治成绩(满分100分,成绩均不低于40分的整数)分成六段:[40,50),[50,60),[60,70),[70,80)[80,90),[90,100]后,得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 课程 人数 | 数学 | 英语 | 物理 | 化学 |
| 100 | √ | × | √ | √ |
| 217 | × | √ | × | √ |
| 200 | √ | √ | √ | × |
| 300 | √ | × | √ | × |
| 85 | √ | × | × | × |
| 98 | × | √ | × | × |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{8}$个单位长度 | B. | 向右平移$\frac{π}{8}$个单位长度 | ||
| C. | 向左平移$\frac{π}{4}$个单位长度 | D. | 向右平移$\frac{π}{4}$个单位长度 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com