
分析 根据反比例函数的单调性,可判断①;判断出函数的图象为散点图,可判断②;根据函数图象的平移变换法则,可判断③;根据抽象函数定义域的求法,可判断④.
解答 解:①函数y=$\frac{1}{x}$的单调减区间是(-∞,0)和(0,+∞),在(-∞,0)∪(0,+∞)不是单调函数,故①错误;
②函数y=2x(x∈N)的图象是一直线上的散点,故②错误;
③函数y=3(x-1)2的图象可由y=3x2的图象向右平移1个单位得到,故③正确;
④若函数f(x)的定义域为[0,2],则由2x∈[0,2]得:x∈[0,1],故函数f(2x)的定义域为[0,1],故④正确;
故答案为:③④.
点评 本题以命题的真假判断与应用为载体,考查了函数的单调性,函数的图象,函数图象的平移变换法则,抽象函数的定义域,难度中档.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | -10 | C. | -14 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
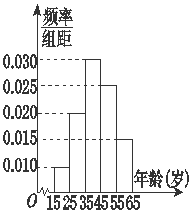 为了宣传在某市举行的“第十届中国艺术节”,筹委会举办了知识有奖问答活动,随机从15~65岁的市民中抽取n人,回答问题统计结果如图表所示:
为了宣传在某市举行的“第十届中国艺术节”,筹委会举办了知识有奖问答活动,随机从15~65岁的市民中抽取n人,回答问题统计结果如图表所示:| 组号 | 分组 | 回答正确 的人数 | 回答正确的人数 占本组的频率 |
| 第1组 | [15,25) | 5 | 0.5 |
| 第2组 | [25,35) | a | 0.9 |
| 第3组 | [35,45) | 27 | x |
| 第4组 | [45,55) | 9 | 0.36 |
| 第5组 | [55,65) | 3 | 0.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com