
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
分析 根据题意,由函数的解析式计算f(1)、f(2)、f(3)、f(4)的值,结合零点存在定理,即可得到所求区间.
解答 解:根据题意,对于函数函数f(x)=ln(x+1)-$\frac{2}{{x}^{2}}$,其定义域为(-1,0)∪(0,+∞),
f(0)不存在,
f(1)=ln2-$\frac{2}{1}$=ln2-1<0,
f(2)=ln3-$\frac{2}{4}$=ln2-$\frac{1}{2}$>0,
f(3)=ln4-$\frac{2}{9}$>0,
f(4)=ln5-$\frac{2}{25}$>0,
由零点存在定理可得,函数f(x)=ln(x+1)-$\frac{2}{{x}^{2}}$的零点所在的大致区间为(1,2);
故选:B.
点评 本题考查二分法的运用,本题解题的关键是求出区间的两个端点的函数值,进行比较.


科目:高中数学 来源: 题型:解答题
 随着互联网的发展,移动支付(又称手机支付)越来越普遍,某学校兴趣小组为了了解移动支付在大众中的熟知度,对15~65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有n个人,把这n个人按照年龄分成5组:第1组[15,25),第2组[25,35),第3组[35,45),第4组[45,55),第5组[55,65),然后绘制成如图所示的频率分布直方图,其中第一组的频数为20.
随着互联网的发展,移动支付(又称手机支付)越来越普遍,某学校兴趣小组为了了解移动支付在大众中的熟知度,对15~65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有n个人,把这n个人按照年龄分成5组:第1组[15,25),第2组[25,35),第3组[35,45),第4组[45,55),第5组[55,65),然后绘制成如图所示的频率分布直方图,其中第一组的频数为20.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | -$\frac{1}{2}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{6}$或$\frac{5π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
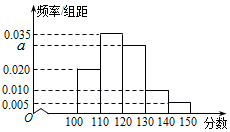 某校从高三年级中随机选取200名学生,将他们的一模数学成绩绘制成频率分布直方图(如图).由图中数据可知a=0.030.若要从成绩在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从成绩在[130,140)内的学生中选取的人数应为4.
某校从高三年级中随机选取200名学生,将他们的一模数学成绩绘制成频率分布直方图(如图).由图中数据可知a=0.030.若要从成绩在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从成绩在[130,140)内的学生中选取的人数应为4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com