
分析 设出矩阵,利用特征向量的定义,即二阶变换矩阵的概念,建立方程组,即可得到结论.
解答 解:由题意,$[\begin{array}{l}{1}&{a}\\{-1}&{b}\end{array}]$$[\begin{array}{l}{1}\\{-1}\end{array}]$=$[\begin{array}{l}{-1}\\{5}\end{array}]$,即$\left\{\begin{array}{l}{1-a=-1}\\{-1-b=-5}\end{array}\right.$,解得a=2,b=4,所以矩阵M=$[\begin{array}{l}{1}&{2}\\{-1}&{4}\end{array}]$.
所以矩阵M的特征多项式为f(λ)=$|\begin{array}{l}{λ-1}&{-2}\\{1}&{λ-4}\end{array}|$=λ2-5λ+6,令f(λ)=0,得矩阵M的特征值为2和3.
点评 本题考查特征值,考查二阶变换矩阵,考查学生的计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若|x-y2|+|x2+y|≤1,则${(x+\frac{1}{2})^2}+{(y-\frac{1}{2})^2}≤\frac{3}{2}$ | |
| B. | 若|x-y2|+|x2-y|≤1,则${(x-\frac{1}{2})^2}+{(y-\frac{1}{2})^2}≤\frac{3}{2}$ | |
| C. | 若|x+y2|+|x2-y|≤1,则${(x+\frac{1}{2})^2}+{(y+\frac{1}{2})^2}≤\frac{3}{2}$ | |
| D. | 若|x+y2|+|x2+y|≤1,则${(x-\frac{1}{2})^2}+{(y+\frac{1}{2})^2}≤\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
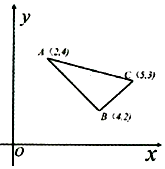 已知点(x,y)在△ABC所包围的阴影区域内(包括边界),若有且仅有B(4,2)是使得z=ax-y取得最大值的最优解,则实数a的取值范围为( )
已知点(x,y)在△ABC所包围的阴影区域内(包括边界),若有且仅有B(4,2)是使得z=ax-y取得最大值的最优解,则实数a的取值范围为( )| A. | -1<a<1 | B. | -1≤a≤1 | C. | -1≤a<1 | D. | -1<a≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com