
【题目】设![]() ,若数列
,若数列![]() 满足:对所有
满足:对所有![]() ,
,![]() ,且当
,且当![]() 时,
时,![]() ,则称
,则称![]() 为“
为“![]() 数列”,设
数列”,设![]() R,函数
R,函数 ,数列
,数列![]() 满足
满足![]() ,
,![]() (
(![]() ).
).
(1)若![]() ,而
,而![]() 是
是![]() 数列,求
数列,求![]() 的值;
的值;
(2)设![]() ,证明:存在
,证明:存在![]() ,使得
,使得![]() 是
是![]() 数列,但对任意
数列,但对任意![]() ,
,![]() 都不是
都不是![]() 数列;
数列;
(3)设![]() ,证明:对任意
,证明:对任意![]() ,都存在
,都存在![]() ,使得
,使得![]() 是
是![]() 数列.
数列.
【答案】(1) ![]() (2)见证明;(3)见证明
(2)见证明;(3)见证明
【解析】
(1)![]() ,
,![]() ,分
,分![]() 两种情况讨论得到
两种情况讨论得到![]() .(2) 先证明当
.(2) 先证明当![]() ,只需
,只需![]() ,即满足
,即满足![]() ,且当
,且当![]() ,
,![]() ,所以是
,所以是![]() 数列,
数列,![]() ,所以不是
,所以不是![]() 数列;再证明当
数列;再证明当![]() ,只需
,只需![]() ,即满足
,即满足![]() ,且当
,且当![]() ,
,![]() ,所以是
,所以是![]() 数列,
数列,![]() ,所以不是
,所以不是![]() 数列.(3)通过归纳得到:当m为奇数,在
数列.(3)通过归纳得到:当m为奇数,在![]() ,
,![]() 有解,存在
有解,存在![]() ;
;
当m为偶数,在![]() ,
,![]() 有解,存在
有解,存在![]() .再结合函数映射性质可知,当
.再结合函数映射性质可知,当![]() 时,
时,![]() ,所以对任意
,所以对任意![]() ,都存在
,都存在![]() ,使得
,使得![]() 是
是![]() 数列.
数列.
(1)![]() ,
,![]() ,当
,当![]() ,
,![]() ,
,![]() ;
;
当![]() ,
,![]() ,
,![]() ,不符;综上所述,
,不符;综上所述,![]() .
.
(2)当![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,既不是
,…,既不是![]() 数列,也不是
数列,也不是![]() 数列;
数列;
当![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,既不是
,…,既不是![]() 数列,也不是
数列,也不是![]() 数列;
数列;
当![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,既不是
,…,既不是![]() 数列,也不是
数列,也不是![]() 数列;
数列;
当![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,只需
,…,只需![]() ,
,
即满足![]() ,且当
,且当![]() ,
,![]() ,∴是
,∴是![]() 数列,
数列,![]() ,∴不是
,∴不是![]() 数列;
数列;
当![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,只需
,…,只需![]() ,
,
即满足![]() ,且当
,且当![]() ,
,![]() ,∴是
,∴是![]() 数列,
数列,![]() ,∴不是
,∴不是![]() 数列;
数列;
综上,存在![]() ,使得
,使得![]() 是
是![]() 数列,但对任意
数列,但对任意![]() ,
,![]() 都不是
都不是![]() 数列.
数列.
(3)![]() ,当
,当![]() ,
,![]() 有解,存在
有解,存在![]() ;
;
![]() ,当
,当![]() ,
,![]() 有解,存在
有解,存在![]() ;
;
![]() ,当
,当![]() ,
,![]() 有解,存在
有解,存在![]() ;
;
![]() ,当
,当![]() ,
,![]() 有解,存在
有解,存在![]() ;
;
……,
当m为奇数,在![]() ,
,![]() 有解,存在
有解,存在![]() ;
;
当m为偶数,在![]() ,
,![]() 有解,存在
有解,存在![]() ;
;
结合函数映射性质可知,当![]() 时,
时,![]() ,
,
∴对任意![]() ,都存在
,都存在![]() ,使得
,使得![]() 是
是![]() 数列.
数列.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:
【题目】某地区不同身高![]() 的未成年男孩的体重平均值
的未成年男孩的体重平均值![]() 如下表:
如下表:
身高 | 60 | 70 | 80 | 90 | 100 |
体重 | 6.13 | 7.90 | 9.99 | 12.15 | 15.02 |
已知![]() 与
与![]() 之间存在很强的线性相关性,
之间存在很强的线性相关性,
(1)据此建立![]() 与
与![]() 之间的回归方程;
之间的回归方程;
(2)若体重超过相同身高男性体重平均值的1.2倍为偏胖,低于0.8倍为偏瘦,那么这个地区一名身高![]() 体重为
体重为![]() 的在校男生的体重是否正常?
的在校男生的体重是否正常?
参考数据:![]() ,
,![]() ,
,![]()
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 是参数),以坐标原点为极点,
是参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 经过伸缩变换
经过伸缩变换![]() 得到曲线
得到曲线![]() ,
,![]() 是曲线
是曲线![]() 上任意一点,求点
上任意一点,求点![]() 到曲线
到曲线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国道路交通安全法》第47条的相关规定:机动车行经人行道时,应当减速慢行;遇行人正在通过人行道,应当停车让行,俗称“礼让斑马线”, 《中华人民共和国道路交通安全法》第90条规定:对不礼让行人的驾驶员处以扣3分,罚款50元的处罚.下表是某市一主干路口监控设备所抓拍的5个月内驾驶员“礼让斑马线”行为统计数据:
月份 | 1 | 2 | 3 | 4 | 5 |
违章驾驶员人数 | 120 | 105 | 100 | 90 | 85 |
(1)请利用所给数据求违章人数![]() 与月份
与月份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(2)预测该路口9月份的不“礼让斑马线”违章驾驶员人数.
参考公式: 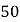 ,
, ![]() .
.
参考数据: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是周期为4的奇函数,且当
是周期为4的奇函数,且当![]() 时,
时,![]() ,方程
,方程![]() 在区间
在区间![]() 内有唯一解
内有唯一解![]() ,则方程
,则方程![]() 在区间
在区间![]() 上所有解的和为( )
上所有解的和为( )
A. ![]() B. 036162C. 3053234D. 3055252
B. 036162C. 3053234D. 3055252
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂在生产产品时需要用到长度为![]() 的
的![]() 型和长度为
型和长度为![]() 的
的![]() 型两种钢管.工厂利用长度为
型两种钢管.工厂利用长度为![]() 的钢管原材料,裁剪成若干
的钢管原材料,裁剪成若干![]() 型和
型和![]() 型钢管,假设裁剪时损耗忽略不计,裁剪后所剩废料与原材料的百分比称为废料率.
型钢管,假设裁剪时损耗忽略不计,裁剪后所剩废料与原材料的百分比称为废料率.
(1)要使裁剪的废料率小于![]() ,共有几种方案剪裁?请写出每种方案中分别被裁剪
,共有几种方案剪裁?请写出每种方案中分别被裁剪![]() 型钢管和
型钢管和![]() 型钢管的根数;
型钢管的根数;
(2)假设一根![]() 型钢管和一根
型钢管和一根![]() 型钢管能成为一套毛胚,假定只能按(1)中的那些方案裁剪,若工厂需要生产
型钢管能成为一套毛胚,假定只能按(1)中的那些方案裁剪,若工厂需要生产![]() 套毛胚,则至少需要采购多少根长度为
套毛胚,则至少需要采购多少根长度为![]() 的钢管原材料?最终的废料率为多少?
的钢管原材料?最终的废料率为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
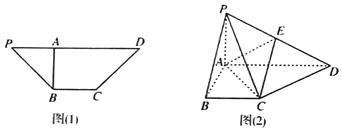
【题目】如图![]() 在四边形PBCD中,
在四边形PBCD中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,沿AB把三角形PAB折起,使P,D两点的距离为10,得到如图
,沿AB把三角形PAB折起,使P,D两点的距离为10,得到如图![]() 所示图形.
所示图形.
![]() Ⅰ
Ⅰ![]() 求证:平面
求证:平面![]() 平面PAC;
平面PAC;
![]() Ⅱ
Ⅱ![]() 若点E是PD的中点,求三棱锥
若点E是PD的中点,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )过点
)过点![]() ,短轴一个端点到右焦点的距离为2.
,短轴一个端点到右焦点的距离为2.
(1)求椭圆C的方程;
(2)设过定点![]() 的直线1与椭圆交于不同的两点A,B,若坐标原点O在以线段AB为直径的圆上,求直线l的斜率k.
的直线1与椭圆交于不同的两点A,B,若坐标原点O在以线段AB为直径的圆上,求直线l的斜率k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一椭圆形溜冰场,长轴长100米,短轴长为60米,现要在这溜冰场上划定一个各顶点都在溜冰场边界上的矩形区域,且使这个区域的面积最大,应把这个矩形的顶点定位在何处?并求出此矩形的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com