
分析 (1)由β=(α+β)-α,利用三角函数恒等变换的应用即可化简得解.
(2)由条件利用两角和差的正弦公式、同角三角函数的基本关系可得2tanβtan2α-tanα+tanβ=0,再根据△=1-4(2tanβ)•tanβ≥0,求得tanβ的最大值.
解答 解:(1)∵sinβ=cos(α+β)sinα,
∴sin[(α+β)-α]=cos(α+β)sinα,
∴sin(α+β)cosα-cos(α+β)sinα=cos(α+β)sinα
∴sin(α+β)cosα=2cos(α+β)sinα,
∴tan(α+β)cotα=2
(2)∵sinβ=cos(α+β)sinα=sinαcosαcosβ-sinβsin2α
∴sinβ(1+sin2α)=sinαcosαcosβ,
∴$tanβ=\frac{sinαcosα}{{1+{{sin}^2}α}}=\frac{sinαcosα}{{2{{sin}^2}α+{{cos}^2}α}}$
即$tanβ=\frac{tanα}{{2{{tan}^2}α+1}}$,
∵2tanβtan2α-tanα+tanβ=0,
∴(-1)2≥4(2tanβ)•tanβ,
∴$tanβ≤\frac{{\sqrt{2}}}{4}$,当且仅当$tanα=\frac{{\sqrt{2}}}{2}$时等号成立.
故tanβ的最大值为:$\frac{\sqrt{2}}{4}$.
点评 本题主要考查了两角和差的正弦公式,同角三角函数的基本关系,考查了计算能力和转化思想,属于中档题.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:选择题
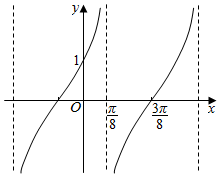 已知函数f(x)=Atan(ωx+φ)$(ω>0,|φ|<\frac{π}{2})$,y=f(x)的部分图象如图,则$f(\frac{π}{24})$=( )π
已知函数f(x)=Atan(ωx+φ)$(ω>0,|φ|<\frac{π}{2})$,y=f(x)的部分图象如图,则$f(\frac{π}{24})$=( )π| A. | 2+$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 2-$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{kπ}{2}$+$\frac{π}{6}$,$\frac{kπ}{2}$+$\frac{5π}{12}$],k∈Z | B. | [$\frac{kπ}{2}$-$\frac{π}{12}$,$\frac{kπ}{2}$+$\frac{π}{6}$],k∈Z | ||
| C. | [kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$],k∈Z | D. | [kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],k∈Z |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com