
| A. | 0 | B. | 1 | C. | 2 | D. | 0或2 |
分析 构造函数F(x)=xg(x)=xf(x)+2,则g(x)的零点即为F(x)的零点,根据导数和函数的奇偶性判断F(x)的单调性,根据F(x)的最值符号判断零点个数.
解答 解:由于函数g(x)=f(x)+$\frac{2}{x}$,可得x≠0,∴g(x)的零点与 xg(x)的零点相同,
令F(x)=xg(x)=xf(x)+2,
∴F′(x)=f(x)+xf′(x),
由于当x>0时,f′(x)+$\frac{f(x)}{x}$=$\frac{xf′(x)+f(x)}{x}<0$,
∴F′(x)=f(x)+xf′(x)<0,
∴F(x)在(0,+∞)上为减函数,
∵f(x)是奇函数,
∴F(x)=xg(x)=xf(x)+2为偶函数.
∵$\underset{lim}{x→0+}$F(x)=$\underset{lim}{x→0+}(xf(x)+2)$=2,
∴当$\underset{lim}{x→+∞}$F(x)≥0时,F(x)无零点,当$\underset{lim}{x→+∞}$F(x)<0时,F(x)有两个零点.
故选:D.
点评 本题考查了函数的零点与单调性,最值的关系,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
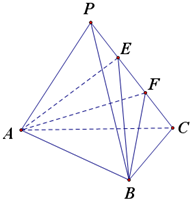 在三棱锥P-ABC中,PA=PB=PC=3,AB=$\sqrt{6}$,BC=$\sqrt{3}$,AB⊥BC,E,F为PC的三等分点.
在三棱锥P-ABC中,PA=PB=PC=3,AB=$\sqrt{6}$,BC=$\sqrt{3}$,AB⊥BC,E,F为PC的三等分点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直线 | B. | 圆 | C. | 线段 | D. | 射线 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com