
分析 (Ⅰ)求出f(x)的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的最大值和最小值即可;
(Ⅱ)令g(x)=f(x)-2ax=(a-$\frac{1}{2}$)x2-2ax+lnx,由题意可得g(x)<0在区间(1,+∞)上恒成立.求出g(x)的导数,对a讨论,①若a>$\frac{1}{2}$,②若a≤$\frac{1}{2}$,判断单调性,求出极值点,即可得到所求范围;
(Ⅲ)由题意可得任意x1∈(0,2),存在x2∈[1,2],只要g(x1)max≤h(x2)max,运用单调性分别求得g(x)和h(x)的最值,解不等式即可得到所求b的范围
解答 解:(Ⅰ)当a=0时,$f(x)=-\frac{1}{2}{x^2}+lnx$,
$f'(x)=-x+\frac{1}{x}=\frac{{-{x^2}+1}}{x}=\frac{-(x+1)(x-1)}{x}$,
令f′(x)>0,解得:0<x<1,令f′(x)<0,解得:x>1,
∴f(x)在区间[$\frac{1}{e}$,1]上是增函数,在[1,e]上为减函数,
∴f(x)max=f(1)=-$\frac{1}{2}$,
又$f(\frac{1}{e})=-1-\frac{1}{{2{e^2}}}$>$f(e)=1-\frac{e^2}{2}$,
∴${f_{min}}(x)=f(e)=1-\frac{e^2}{2}$;
(2)令g(x)=f(x)-2ax=(a-$\frac{1}{2}$)x2-2ax+lnx,
则g(x)的定义域为(0,+∞).
在区间(1,+∞)上,函数f(x)的图象恒在直线y=2ax下方
等价于g(x)<0在区间(1,+∞)上恒成立.g′(x)=(2a-1)x-2a+$\frac{1}{x}$=$\frac{(x-1)[(2a-1)x-1]}{x}$①,
①若a>$\frac{1}{2}$,令g'(x)=0,得极值点x1=1,x2=$\frac{1}{2a-1}$,
当x2>x1=1,即$\frac{1}{2}$<a<1时,在(0,1)上有g'(x)>0,
在(1,x2)上有g'(x)<0,在(x2,+∞)上有g'(x)>0,
此时g(x)在区间(x2,+∞)上是增函数,
并且在该区间上有g(x)∈(g(x2),+∞),不合题意;
当x2≤x1=1,即a≥1时,同理可知,g(x)在区间(1,+∞)上,
有g(x)∈(g(1),+∞),也不合题意;
②若a≤$\frac{1}{2}$,则有2a-1≤0,此时在区间(1,+∞)上恒有g'(x)<0,
从而g(x)在区间(1,+∞)上是减函数;
要使g(x)<0在此区间上恒成立,只须满足g(1)=-a-$\frac{1}{2}$≤0⇒a≥-$\frac{1}{2}$,
由此求得a的范围是[-$\frac{1}{2}$,$\frac{1}{2}$].
综合①②可知,当a∈[-$\frac{1}{2}$,$\frac{1}{2}$]时,函数f(x)的图象恒在直线y=2ax下方;
(3)当a=$\frac{2}{3}$时,由(Ⅱ)中①知g(x)在(0,1)上是增函数,
在(1,2)上是减函数,所以对任意x1∈(0,2),都有g(x1)≤g(1)=-$\frac{7}{6}$,
又已知存在x2∈[1,2],使g(x1)≤h(x2),
即存在x2∈[1,2],使x2-2bx+$\frac{19}{6}$≥-$\frac{7}{6}$,即存在x2∈[1,2],2bx≤x2+$\frac{13}{3}$,
即存在x2∈[1,2],使2b≤x+$\frac{13}{3x}$.
因为y=x+$\frac{13}{3x}$∈[$\frac{25}{6}$,$\frac{16}{3}$](x∈[1,2]),
所以2b≤$\frac{16}{3}$,解得b≤$\frac{8}{3}$,所以实数b的取值范围是(-∞,$\frac{8}{3}$].
点评 本题考查导数的运用:求切线的方程和单调性,考查不等式恒成立问题及任意性和存在性问题,注意转化为求最值问题,考查运算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
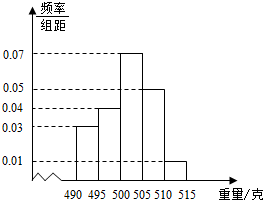 某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的重量(单位:克).重量的分组区间为(490,495],(495,500],…,(510,515],由此得到样本的频率分布直方图,如图.
某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的重量(单位:克).重量的分组区间为(490,495],(495,500],…,(510,515],由此得到样本的频率分布直方图,如图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | $\frac{\sqrt{7}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com