
如图四棱锥S﹣ABCD中,SD⊥AD,SD⊥CD,E是SC的中点,O是底面正方形ABCD的中心,AB=SD=6.

(1)求证:EO∥平面SAD;
(2)求直线EO与平面SCD所成的角.
(1)见解析;(2)45°
【解析】
试题分析:(1)利用三角形中位线的性质,可得线线平行,从而可得线面平行;
(2)根据EO∥SA,可得直线EO与平面SCD所成的角等于直线SA与平面SCD所成的角,证明AD⊥平面SCD,可得∠ASD为直线SA与平面SCD所成的角,从而可得结论.
(1)证明:∵E是SC的中点,O是底面正方形ABCD的中心,
∴EO∥SA
∵EO?平面SAD,SA?平面SAD,
∴EO∥平面SAD;
(2)【解析】
∵EO∥SA
∴直线EO与平面SCD所成的角等于直线SA与平面SCD所成的角
∵SD⊥AD,SD⊥CD,AD∩CD=D
∴SD⊥平面ABCD
∵AD?平面ABCD
∴SD⊥AD
∵AD⊥DC,SD∩DC=D
∴AD⊥平面SCD
∴∠ASD为直线SA与平面SCD所成的角
∵AB=SD
∴∠ASD=45°
∴直线EO与平面SCD所成的角等于45°.


科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.1线性变换与二阶矩阵练习卷(解析版) 题型:填空题
将曲线  ,上所有点的横坐标扩大到原来的2倍,纵坐标缩小到原来的
,上所有点的横坐标扩大到原来的2倍,纵坐标缩小到原来的 倍后,得到的曲线的焦点坐标为 .
倍后,得到的曲线的焦点坐标为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.1线性变换与二阶矩阵练习卷(解析版) 题型:选择题
抛物线y2=2px,(p>0)绕焦点依逆时针方向旋转90°所得抛物线方程为( )
A.x2=2py
B.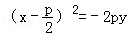
C.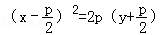
D.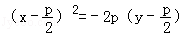
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.1线性变换与二阶矩阵练习卷(解析版) 题型:选择题
对于函数f(x),如果存在锐角θ使得f(x)的图象绕坐标原点逆时针旋转角θ,所得曲线仍是一函数,则称函数f(x)具备角θ的旋转性,下列函数具有角 的旋转性的是( )
的旋转性的是( )
A. B.y=lnx C.
B.y=lnx C. D.y=x2
D.y=x2
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 3.2平面与圆柱面的截线练习卷(解析版) 题型:填空题
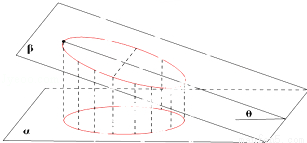
如图,一个底面半径为R的圆柱被与其底面所成角为θ(0°<θ<90°)的平面所截,截面是一个椭圆,
当θ为30°时,这个椭圆的离心率为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 3.2平面与圆柱面的截线练习卷(解析版) 题型:填空题
底面直径为12cm的圆柱被与底面成30°的平面所截,截口是一个椭圆,该椭圆的长轴长 ,短轴长 ,离心率为 .

查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷(解析版) 题型:填空题
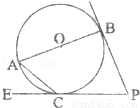
(2014•河东区二模)如图,AB是⊙O的直径,PB,PC分别切⊙O于B,C,若∠ACE=38°,则∠P= .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.1圆周角定理练习卷(解析版) 题型:选择题
图中∠BOD的度数是( )
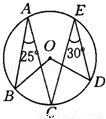
A.55° B.110° C.125° D.150°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com