
分析 (Ⅰ)利用诱导公式和二倍角公式将f(x)化简为f(x)=sin(2x-$\frac{π}{3}$),由周期公式求得周期T;
(Ⅱ)将f($\frac{C}{2}$+$\frac{π}{6}$)=$\frac{1}{2}$代入求得sinC的值,利用正弦定理,求得a的值,由三角形的内角和定理,求得sinB的值,利用三角形的面积公式S=$\frac{1}{2}$acsinB,即可求得.
解答 解:(Ⅰ)f(x)=2sin(x-$\frac{π}{6}$)sin(x+$\frac{π}{3}$),x∈R.
=-2cos(x-$\frac{π}{6}$+$\frac{π}{2}$)sin(x+$\frac{π}{3}$),
=-sin[2(x+$\frac{π}{3}$)],
=-sin(2x+$\frac{2π}{3}$),
=sin(2x-$\frac{π}{3}$),
函数f(x)的最小正周期T=$\frac{2π}{ω}$=π,
∴函数f(x)的最小正周期T=π,
(Ⅱ)f($\frac{C}{2}$+$\frac{π}{6}$)=$\frac{1}{2}$,
sin[2($\frac{C}{2}$+$\frac{π}{6}$)-$\frac{π}{3}$]=$\frac{1}{2}$,
sinC=$\frac{1}{2}$,锐角C,C=$\frac{π}{6}$,
由正弦定理,$\frac{a}{sinA}=\frac{c}{sinC}$,a=2$\sqrt{2}$,
B=π-(A+C)=,
sinB=sin[π-(A+C)]=sin(A+C)=sinAcosC+cosAsinB=$\frac{\sqrt{6}+\sqrt{2}}{4}$,
由三角形面积公式S,S=$\frac{1}{2}$acsinB=$\frac{1}{2}$×2×2$\sqrt{2}$×$\frac{\sqrt{6}+\sqrt{2}}{4}$,
=1+$\sqrt{3}$.
点评 本题主要考查两角和差的正弦公式、二倍角公式、同角三角函数的基本关系,二倍角公式的应用,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届江苏南京市高三上学期学情调研数学试卷(解析版) 题型:解答题
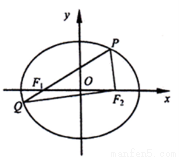
如图,在平面直角坐标系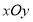 中,椭圆
中,椭圆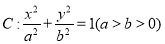 的左、右焦点分别为
的左、右焦点分别为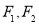 ,
,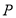 为椭圆上一点(在
为椭圆上一点(在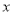 轴上方),连结
轴上方),连结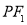 并延长交椭圆于另一点
并延长交椭圆于另一点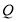 ,设
,设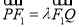 .
.
(1)若点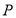 的坐标为
的坐标为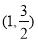 ,且
,且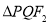 的周长为8,求椭圆
的周长为8,求椭圆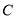 的方程;
的方程;
(2)若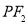 垂直于
垂直于 轴,且椭圆
轴,且椭圆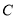 的离心率
的离心率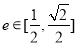 ,求实数
,求实数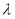 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com