Question

17．过正四棱锥（侧棱长全是1，侧面三角形的顶角为30度）的底面一个顶点的平面截棱锥所得四边形的周长的最小值是（　　）

• A． 1
• B． 2
• C． $\sqrt{2}$
• D． $\sqrt{3}$

Answer 1

分析 把正四棱锥的四个侧面以顶点为公共点展开，容易得出截棱锥所得四边形的周长的最小值是什么．

解答 解：如图所示，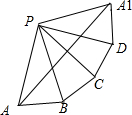

把正四棱锥P-ABCD的四个侧面以顶点为公共点展开，
连接AA₁，则AA₁是截棱锥所得四边形的周长的最小值；
又PA=PA₁，∠APA₁=4×30°=120°，
∴${{AA}_{1}}^{2}$=PA²+${{PA}_{1}}^{2}$-2PA•PA₁•cos120°
=1²+1²-2×1×1×（-$\frac{1}{2}$）
=3，
∴AA₁=$\sqrt{3}$；
即截棱锥所得四边形的周长最小值是$\sqrt{3}$．
故选：D．

点评 本题考查了空间几何体的平面展开图的应用问题，也考查了转化思想的应用问题，是基础题目．