Question

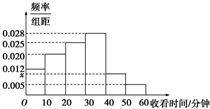
4．某电视传媒公司为了了解某类体育节目的收视情况，随机抽取了100名观众进行调查，如图是根据调查结果绘制的观众日均收看该类体育节目时间的频率分布直方图，其中收看时间分组区间是：[0，10），[10，20），[20，30），[30，40），[40，50），[50，60]．将日均收看该类体育节目时间不低于40分钟的观众称为“体育迷”，则图中x的值为（　　）

• A． 0.01
• B． 0.02
• C． 0.03
• D． 0.04

Answer 1

分析 利用频率之和为1，建立方程，可得图中x的值．

解答 解：由题设可知（0.005+x+0.012+0.02+0.025+0.028）×10=1，
解之得x=0.01，
故选：A．

点评 本题考查了频率分布直方图问题，关键是掌握长方形的面积之和等于1，属于基础题．