
分析 (I)利用递推式即可得出;
(II)利用“放缩法”、“错位相减法”、等比数列的前n项和公式即可得出.
解答 (Ⅰ)解:∵数列{an}满足a13+a23+…+an3=$\frac{{n}^{2}(n+1)^{2}}{4}$,n∈N*.
∴当n=1时,${a}_{1}^{3}$=1,解得a1=1.
当n≥2时,满足a13+a23+…+${a}_{n-1}^{3}$=$\frac{{n}^{2}(n-1)^{2}}{4}$,n∈N*.
∴${a}_{n}^{3}$=$\frac{{n}^{2}(n+1)^{2}}{4}$-$\frac{{n}^{2}(n-1)^{2}}{4}$=n3,n∈N*.
解得an=n,
当n=1时也满足,
∴an=n.
(Ⅱ)证明:由(Ⅰ)得$\frac{{a}_{n}}{{2}^{{a}_{n}}-{a}_{n}}$=$\frac{n}{{2}^{n}-n}$.
∵2n+1-(n+1)2n-n+(2n-1)>2n-n≥2-1>0,
∴$\frac{{a}_{n}}{{2}^{{a}_{n}}-{a}_{n}}$>0.
又$\frac{{a}_{n}}{{2}^{{a}_{n}}-{a}_{n}}$-$\frac{2n}{{2}^{n}}$=$\frac{2n(n-{2}^{n-1})}{n({2}^{n}-n)}$≤0.
∴$\frac{{a}_{n}}{{2}^{{a}_{n}}-{a}_{n}}$≤$\frac{n}{{2}^{n-1}}$.
∴$\frac{{a}_{1}}{{2}^{{a}_{1}}-{a}_{1}}$+$\frac{{a}_{2}}{{2}^{{a}_{2}}-{a}_{2}}$+$\frac{{a}_{3}}{{2}^{{a}_{3}}-{a}_{3}}$+…+$\frac{{a}_{n}}{{2}^{{a}_{n}}-{a}_{n}}$<$\frac{1}{{2}^{1-1}}$+$\frac{2}{{2}^{2-1}}+\frac{3}{{2}^{3-1}}$+…+$\frac{n}{{2}^{n-1}}$.
设S=$\frac{1}{{2}^{1-1}}$+$\frac{2}{{2}^{2-1}}+\frac{3}{{2}^{3-1}}$+…+$\frac{n}{{2}^{n-1}}$,
$\frac{1}{2}S$=$\frac{1}{2}+\frac{2}{{2}^{2}}$+…+$\frac{n-1}{{2}^{n-1}}+\frac{n}{{2}^{n}}$,
由错位相减法,得$\frac{1}{2}S$=1+$\frac{1}{2}+\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n-1}}-\frac{n}{{2}^{n}}$=$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$-$\frac{n}{{2}^{n}}$=2-$\frac{2+n}{{2}^{n}}$<2,
∴S<4.
∴$\frac{{a}_{1}}{{2}^{{a}_{1}}-{a}_{1}}$+$\frac{{a}_{2}}{{2}^{{a}_{2}}-{a}_{2}}$+$\frac{{a}_{3}}{{2}^{{a}_{3}}-{a}_{3}}$+…+$\frac{{a}_{n}}{{2}^{{a}_{n}}-{a}_{n}}$<4.
点评 题考查了“错位相减法”、等比数列的前n项和公式、递推式的应用、“放缩法”,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<1} | B. | {x|x≥-2} | C. | {x|-2≤x<1} | D. | {x|-1<x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ | B. | $\frac{8}{3}$ | C. | 3 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 既不充分又不必要条件 | D. | 充要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
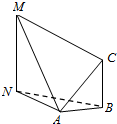 如图,为测量山高MN,选择A和另一座山的山顶|PA|为测量观测点.从△ABC点测得MB=MC点的俯角∠NMA=30°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°已知山高BC=200m,则山高MN=300m.
如图,为测量山高MN,选择A和另一座山的山顶|PA|为测量观测点.从△ABC点测得MB=MC点的俯角∠NMA=30°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°已知山高BC=200m,则山高MN=300m.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | -$\frac{4}{3}$ | D. | -$\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com