
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
分析 由题意令h(x)=$\frac{g(x)}{|x|+1}$,h(x)=$\frac{g(x)}{|x|+1}$的最大最小值分别为M-2,m-2,由奇函数的性质可得(M-2)+(m-2)=0,变形可得答案.
解答 解:∵函数y=g(x)为奇函数,∴g(-x)=-g(x),
f(x)=$\frac{2|x|+g(x)+2}{|x|+1}$=2+$\frac{g(x)}{|x|+1}$,
令h(x)=$\frac{g(x)}{|x|+1}$,则h(-x)=-$\frac{g(x)}{|x|+1}$=-h(x),即y=h(x)为奇函数,
∵函数f(x)=$\frac{2|x|+g(x)+2}{|x|+1}$(x∈R)有最大值为M,最小值为m
∴h(x)=$\frac{g(x)}{|x|+1}$的最大最小值分别为M-2,m-2,
由奇函数的性质可得(M-2)+(m-2)=0,
解得M+m=4.
故选:D.
点评 本题考查函数的奇偶性,涉及函数的最值问题,属中档题.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:填空题
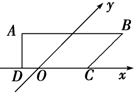 如图所示,ABCD是一平面图形的水平放置的斜二测直观图,在斜二测直观图中,ABCD是一直角梯形,AB∥CD,AD⊥CD,且BC与y轴平行,若AB=6,DC=4,AD=2,则这个平面图形的实际面积是20$\sqrt{2}$.
如图所示,ABCD是一平面图形的水平放置的斜二测直观图,在斜二测直观图中,ABCD是一直角梯形,AB∥CD,AD⊥CD,且BC与y轴平行,若AB=6,DC=4,AD=2,则这个平面图形的实际面积是20$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18 | B. | $12+8\sqrt{2}$ | C. | $12+2\sqrt{2}$ | D. | $12+4\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10π | B. | $\frac{31}{3}$π | C. | $\frac{32}{3}$π | D. | 11π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
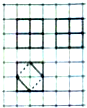 如图,网格纸上小正方形的边长为1,粗线画出的是由正方形切割而成的几何体的三视图,则该几何体的体积为( )
如图,网格纸上小正方形的边长为1,粗线画出的是由正方形切割而成的几何体的三视图,则该几何体的体积为( )| A. | $\frac{11}{2}$ | B. | $\frac{13}{2}$ | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com