考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:几何法:
(Ⅰ)取BC中点O,连结AO,由正三角形的性质得AO⊥BC.由线面垂直的AO⊥BD,由正方形的性质得B
1O⊥BD从而得到BD⊥AB
1,由此能证明AB
1⊥A
1D.
(Ⅱ)由题意知
S△A1BD=
,S
△BCD=1.A
1到平面BCC
1B
1的距离为
,由此利用等积法能求出点C到平面A
1BD的距离.
向量法:
(Ⅰ)取B
1C
1中点O
1,以O为原点,
,
,
的方向为x,y,z轴的正方向,建立空间直角坐标系,利用向量法能证明AB
1⊥A
1D.
(Ⅱ)求出平面A
1BD的法向量和
,由此利用向量法能求出点C到平面A
1BD的距离.
解答:
几何法:
(Ⅰ)证明:取BC中点O,连结AO.
∵△ABC为正三角形,∴AO⊥BC.
∵正三棱柱ABC-A
1B
1C
1中,平面ABC⊥平面BCC
1B
1,
∴AO⊥平面BCC
1B
1,∴AO⊥BD.
连结B
1O,在正方形BB
1C
1C中,O,D分别为BC,CC
1的中点,∴B
1O⊥BD.
∴BD⊥平面AB
1O.∴BD⊥AB
1.(4分 )
又在正方形ABB
1A
1中,AB
1⊥A
1B,又BD∩A
1B=B,
∴AB
1⊥平面A
1BD.∴AB
1⊥A
1D.(6分)
(Ⅱ)解:△A
1BD中,BD=A
1D=
,A
1B=2
,
∴
S△A1BD=
,S
△BCD=1.
在正三棱柱中,A
1到平面BCC
1B
1的距离为
.(9分)
设点C到平面A
1BD的距离为d.
由VA
1-BCD=VC-A
1BD得
S
△BCD•
=
S△A
1BD•d,(10分)
∴d=
=
.
∴点C到平面A
1BD的距离为
.(12分)
向量法:
(Ⅰ)证明:取BC中点O,连结AO.
∵△ABC为正三角形,∴AO⊥BC.
∵在正三棱柱ABC-A
1B
1C
1中,
平面ABC⊥平面BCC
1B
1,∴AD⊥平面BCC
1B
1.
取B
1C
1中点O
1,以O为原点,
,
,
的方向为x,y,z轴的正方向,
建立空间直角坐标系,
则B(1,0,0),D(-1,1,0),
A
1(0,2,
),A(0,0,
),B
1(1,2,0),(4分)
∴
=(1,2,-
),
=(-1,-1,-
).
∵
•
=-1-2+3=0,∴
⊥
.
∴AB
1⊥A
1D.(6分)
(Ⅱ)解:设平面A
1BD的法向量为
=(x,y,z).
=(-1,-1,-
),
=(-2,1,0).
∵
⊥
,
⊥
,
∴
,∴
令x=1,得
=(1,2,-
)为平面A
1BD的一个法向量.(9分)
∵
=(-2,0,0),
∴点C到平面A
1BD的距离d=
=
=.(12分).
点评:本题考查异面直线垂直的证明,考查点到平面的距离的求法,解题时要认真审题,注意空间思维能力的培养.

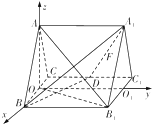
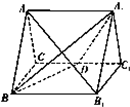 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.


 全优点练单元计划系列答案
全优点练单元计划系列答案 如图,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=DE=1,CD=2,M为CE上的点.
如图,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=DE=1,CD=2,M为CE上的点. 如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AD=1,点M是SD的中点,AN⊥SC,交SC于点N.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AD=1,点M是SD的中点,AN⊥SC,交SC于点N.