
 如图,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=DE=1,CD=2,M为CE上的点.
如图,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=DE=1,CD=2,M为CE上的点.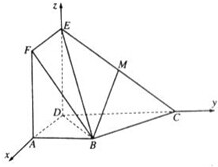 (Ⅰ)证明:在矩形ADEF中,ED⊥AD,
(Ⅰ)证明:在矩形ADEF中,ED⊥AD,| 2 |
| 2 |
| 1 |
| 2 |
| BF |
| EF |
| BM |
| 1 |
| 2 |
| m |
|
| m |
| m |
| BM |
| ||
| 10 |
| ||
| 10 |


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、{x|-3<x<-2} |
| B、{x|2<x<3} |
| C、{x|-4<x<-2或2<x<3} |
| D、{x|3<x<4} |
查看答案和解析>>
科目:高中数学 来源: 题型:
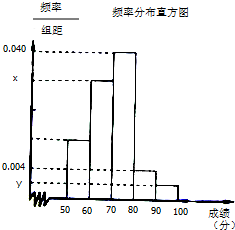 某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成的频率分布表和频率分布直方图(如图所示)解决下列问题:
某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成的频率分布表和频率分布直方图(如图所示)解决下列问题:| 组别 | 分组 | 频数 | 频率 |
| 第1组 | [50,60) | 8 | 0.16 |
| 第2组 | [60,70) | a | |
| 第3组 | [70,80) | 20 | 0.40 |
| 第4组 | [80,90) | 0.08 | |
| 第5组 | [90,100) | 2 | b |
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,底面是等腰梯形的四棱锥E-ABCD中,EA⊥平面ABCD,AB∥CD,AB=2CD,∠ABC=
如图,底面是等腰梯形的四棱锥E-ABCD中,EA⊥平面ABCD,AB∥CD,AB=2CD,∠ABC=| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 将边长为4的正方形ABCD和等腰直角三角形ABE按图拼为新的几何图形,△ABE中,AB=AE,连结DE,CE,若DE=4
将边长为4的正方形ABCD和等腰直角三角形ABE按图拼为新的几何图形,△ABE中,AB=AE,连结DE,CE,若DE=4| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
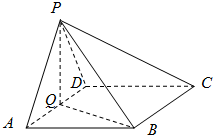 如图,在四棱锥中P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
如图,在四棱锥中P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com