
【题目】已知函数![]() ,其中
,其中![]() .
.
(I)若a=1,求![]() 在区间[0,3]上的最大值和最小值;
在区间[0,3]上的最大值和最小值;
(II)解关于x的不等式![]() .
.
【答案】(Ⅰ)最小值为![]() ,最大值为
,最大值为![]() ;(Ⅱ)答案见解析.
;(Ⅱ)答案见解析.
【解析】试题分析:(1)当![]() 时,
时, ![]() ,根据二次函数的性质能求出
,根据二次函数的性质能求出![]() 在
在![]() 上的最大值和最小值;(2)当
上的最大值和最小值;(2)当![]() 时,原不等式等价于
时,原不等式等价于![]() ,当
,当![]() 时,原不等式等价于
时,原不等式等价于![]() ,由此根据一元二次不等式的解法能求出当
,由此根据一元二次不等式的解法能求出当![]() 时,不等式的解集为
时,不等式的解集为![]() 或
或![]() ,当
,当![]() 时,不等式的的解集为
时,不等式的的解集为![]() ;当
;当![]() 时,不等式的解集为
时,不等式的解集为![]() ;当
;当![]() 时,不等式的解集为
时,不等式的解集为![]() .
.
试题解析:(![]() )当
)当![]() 时,
时, ![]() ,
,
∴函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
∴![]() 在
在![]() 上的最小值为
上的最小值为![]() ,
,
又![]() ,
, ![]() ,
, ![]() ,
,
∴![]() 在
在![]() 上的最大值为
上的最大值为![]() .
.
(![]() )(i)当
)(i)当![]() 时,原不等式等价于
时,原不等式等价于![]() ,
,
∵![]() ,
,
∴![]() ,
,
此时![]() 的解集为
的解集为![]() 或
或![]() .
.
(ii)当![]() 时,原不等式等价于
时,原不等式等价于![]() ,
,
由![]() ,得:
,得:
①若![]() ,则
,则![]() ,此时
,此时![]() 的解集为
的解集为![]() ;
;
②当![]() ,原不等式无解;
,原不等式无解;
③当![]() ,则
,则![]() ,此时,
,此时, ![]() 的解集为
的解集为![]() ,
,
综上,当![]() 时,不等式的解集为
时,不等式的解集为![]() 或
或![]() ,
,
当![]() 时,不等式的解集为
时,不等式的解集为![]() ,
,
当![]() 时,不等式的解集为
时,不等式的解集为![]() ,
,
当![]() 时,不等式的解集为
时,不等式的解集为![]() .
.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系 ![]() 中,直线 的参数方程为
中,直线 的参数方程为  (
( ![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆 ![]() 的极坐标方程为
的极坐标方程为 ![]() .
.
(1)写出圆 ![]() 的直角坐标方程;
的直角坐标方程;
(2)![]() 为直线
为直线 ![]() 上一动点,当
上一动点,当 ![]() 到圆心
到圆心 ![]() 的距离最小时,求
的距离最小时,求 ![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是公差不为零的等差数列,满足
是公差不为零的等差数列,满足![]() 数列
数列![]() 的通项公式为
的通项公式为![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)将数列![]() ,
,![]() 中的公共项按从小到大的顺序构成数列
中的公共项按从小到大的顺序构成数列![]() ,请直接写出数列
,请直接写出数列![]() 的通项公式;
的通项公式;
(3)记![]() ,是否存在正整数
,是否存在正整数![]()
![]() ,使得
,使得![]() 成等差数列?若存在,求出
成等差数列?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,
, ![]() (
( ![]() 为自然对数的底数).
为自然对数的底数).
(1)设曲线 ![]() 在
在 ![]() 处的切线为
处的切线为 ![]() ,若
,若 ![]() 与点
与点 ![]() 的距离为
的距离为 ![]() ,求
,求 ![]() 的值;
的值;
(2)若对于任意实数 ![]() ,
, ![]() 恒成立,试确定
恒成立,试确定 ![]() 的取值范围;
的取值范围;
(3)当 ![]() 时,函数
时,函数 ![]() 在
在 ![]() 上是否存在极值?若存在,请求出极值;若不存在,请说明理由.
上是否存在极值?若存在,请求出极值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨标准煤)的几组对照数据,
(吨标准煤)的几组对照数据,

(1)求![]() ,
, ![]() ,
,
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)已知该厂技动前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
已知![]() ,
, ![]() .
.
 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,若a2+c2+ ![]() ac=b2 , sinA=
ac=b2 , sinA= ![]() .
.
(1)求sinC的值;
(2)若a=2,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项不为零的数列{an}的前n项和为Sn , 且a1=1,Sn=panan+1(n∈N*),p∈R.
(1)若a1 , a2 , a3成等比数列,求实数p的值;
(2)若a1 , a2 , a3成等差数列,
①求数列{an}的通项公式;
②在an与an+1间插入n个正数,共同组成公比为qn的等比数列,若不等式(qn)(n+1)(n+a)≤e对任意的n∈N*恒成立,求实数a的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某淘宝商城在2017年前7个月的销售额![]() (单位:万元)的数据如下表,已知
(单位:万元)的数据如下表,已知![]() 与
与![]() 具有较好的线性关系.
具有较好的线性关系. 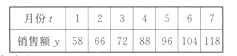
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)分析该淘宝商城2017年前7个月的销售额的变化情况,并预测该商城8月份的销售额.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
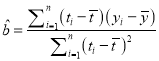 ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com