
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{4}$ | D. | $\frac{1}{4}$ |
分析 把已知等式两边同时乘以x,得到[x2f(x)]′=1,令x2f(x)=x+c,由f(1)=2求得c值,则函数解析式可求,然后利用二次函数求最值.
解答 解:∵xf′(x)+2f(x)=$\frac{1}{x}$,
∴x2f′(x)+2xf(x)=1,
∴[x2f(x)]′=1,
∴x2f(x)=x+c,
将x=1代入可得:
f(1)=1+c=2,得c=1,
∴x2f(x)=x+1,
∴f(x)=$\frac{x+1}{{x}^{2}}=\frac{1}{{x}^{2}}+\frac{1}{x}$,
∴当$\frac{1}{x}=-\frac{1}{2}$,即x=-2时,$f(x)_{min}=-\frac{1}{4}$.
故选:C.
点评 本题考查的知识点是导数的运算,导数在求函数最值时的应用,关键是合理构造函数,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | $[{-π,-\frac{5π}{6}}]$ | B. | $[{-\frac{π}{3},0}]$ | C. | $[{-\frac{2π}{3},-\frac{π}{6}}]$ | D. | $[{-\frac{π}{3},-\frac{π}{6}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
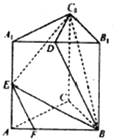 在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,且D,E分别是棱A1B1,A1A1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.
在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,且D,E分别是棱A1B1,A1A1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
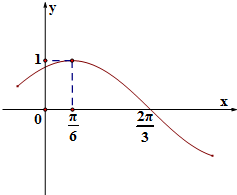 已知函数f(x)=Asin(ωx+φ)(-$\frac{π}{2}$<φ<$\frac{π}{2}$,ω>0,A>0)其部分图象如图所示:
已知函数f(x)=Asin(ωx+φ)(-$\frac{π}{2}$<φ<$\frac{π}{2}$,ω>0,A>0)其部分图象如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com