
已知函数 ,其图象在点
,其图象在点 处的切线方程为
处的切线方程为
(1)求 的值;
的值;
(2)求函数 的单调区间,并求出
的单调区间,并求出 在区间[-2,4]上的最大值.
在区间[-2,4]上的最大值.
(1) a=1,b=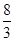 . (2)8.
. (2)8.
解析试题分析:(1)f′(x)=x2-2ax+a2-1, 2分
∵(1,f(1))在x+y-3=0上,∴f(1)=2, 3分
∵(1,2)在y=f(x)的图象上,∴2=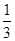 -a+a2-1+b,
-a+a2-1+b,
又f′(1)=-1,∴a2-2a+1=0,
解得a=1,b=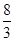 . 6分
. 6分
(2)∵f(x)=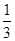 x3-x2+
x3-x2+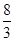 ,∴f′(x)=x2-2x,
,∴f′(x)=x2-2x,
由f′(x)=0可知x=0和x=2是f(x)的极值点,所以有
8分x (-∞,0) 0 (0,2) 2 (2,+∞) f′(x) + 0 - 0 + f(x) ? 极大值 ? 
极小值 ? 
所以f(x)的单调递增区间是(-∞,0)和(2,+∞),单调递减区间是(0,2). 10分
∵f(0)=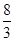 ,f(2)=
,f(2)=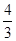 ,f(-2)=-4,f(4)=8,
,f(-2)=-4,f(4)=8,
∴在区间[-2,4]上的最大值为8. 13分
考点:导数的几何意义;利用导数研究函数的单调性;利用导数研究函数的最值。
点评:我们要灵活应用导数的几何意义求曲线的切线方程,尤其要注意切点这个特殊点,充分利用切点即在曲线方程上,又在切线方程上,切点处的导数等于切线的斜率这些条件列出方程组求解。属于基础题。


科目:高中数学 来源: 题型:解答题
(本小题14分)已知函数 ,设
,设 。
。
(Ⅰ)求F(x)的单调区间;
(Ⅱ)若以 图象上任意一点
图象上任意一点 为切点的切线的斜率
为切点的切线的斜率 恒成立,求实数
恒成立,求实数 的最小值。
的最小值。
(Ⅲ)是否存在实数 ,使得函数
,使得函数 的图象与
的图象与 的图象恰好有四个不同的交点?若存在,求出
的图象恰好有四个不同的交点?若存在,求出 的取值范围,若不存在,说名理由。
的取值范围,若不存在,说名理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
设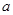 ∈R,函数
∈R,函数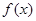 =
=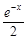 (
(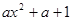 ),其中e是自然对数的底数.
),其中e是自然对数的底数.
(1)判断f (x)在R上的单调性;
(2)当– 1 <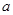 < 0时,求f (x)在[1,2]上的最小值.
< 0时,求f (x)在[1,2]上的最小值.
选做题:请考生从给出的3道题中任选一题做答,并在答题卡上把所选题目的题号用2B铅笔涂黑.注意所做题目的题号必须与所涂的题号一致,在答题卡选答区域指定位置答题.如果多做,则按所做的第一题计分.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
若函数 对任意的实数
对任意的实数 ,
, ,均有
,均有 ,则称函数
,则称函数 是区间
是区间 上的“平缓函数”.
上的“平缓函数”.
(1) 判断 和
和 是不是实数集R上的“平缓函数”,并说明理由;
是不是实数集R上的“平缓函数”,并说明理由;
(2) 若数列 对所有的正整数
对所有的正整数 都有
都有  ,设
,设 ,
,
求证:  .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com