
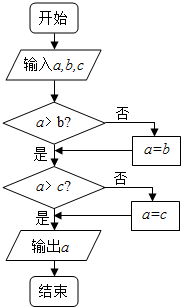
 已知函数f(x)=2x+x,g(x)=log2x+x,h(x)=log5x+x的零点依次为x1、x2、x3,若在如图所示的算法中,另a=x1,b=x2,c=x3,则输出的结果是( )
已知函数f(x)=2x+x,g(x)=log2x+x,h(x)=log5x+x的零点依次为x1、x2、x3,若在如图所示的算法中,另a=x1,b=x2,c=x3,则输出的结果是( )| A. | x1 | B. | x2 | C. | x3 | D. | x2或x3 |
分析 根据零点存在定理,分别求三个函数的零点,判断零点的范围,由程序算法的功能即可得解.
解答 解:函数f(x)=2x+x,f(-1)=$\frac{1}{2}$-1=-$\frac{1}{2}$<0,f(0)=1>0,可知函数的零点x1<0;
函数g(x)=log2x+x=0,g($\frac{1}{2}$)=-1+$\frac{1}{2}$=-$\frac{1}{2}$<0,g(1)=1>0,
可得函数的零点满足:$\frac{1}{2}$<x2<1,
函数h(x)=log5x+x=0,h($\frac{1}{5}$)=-1+$\frac{1}{5}$=-$\frac{4}{5}$<0,h($\frac{1}{2}$)=log5$\frac{1}{2}$+$\frac{1}{2}$=$\frac{lg\frac{5}{4}}{2lg5}$>0,
可得函数的零点满足:$\frac{1}{5}$<x3<$\frac{1}{2}$,
则x1<x3<x2,
模拟执行程序算法,可得程序算法的功能是输出三个数中最大的数,
由题意可得:x2.
故选:B.
点评 本题考查的重点是函数的零点及个数的判断,基本初等函数的单调性的应用,解题的关键是利用零点存在定理,确定零点的值或范围.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
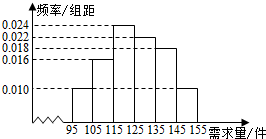 某商场经销某一种电器商品,在一个销售季度内,每售出一件该商品获利200元,未售出的商品,每件亏损100元,根据以往资料,得到销售季度内市场需求量的频率分布直方图,如图所示,现在经销商为下一个销售季度购进了125件该种电器,以n(单位:件;95≤n≤155)表示下一个销售季度市场需求量,Y(单位:元)表示下一个销售季度内销售 该电器的利润.
某商场经销某一种电器商品,在一个销售季度内,每售出一件该商品获利200元,未售出的商品,每件亏损100元,根据以往资料,得到销售季度内市场需求量的频率分布直方图,如图所示,现在经销商为下一个销售季度购进了125件该种电器,以n(单位:件;95≤n≤155)表示下一个销售季度市场需求量,Y(单位:元)表示下一个销售季度内销售 该电器的利润.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com