
已知a=(3,4),b=(4,3),求x、y的值使(xa+yb)⊥a,且|xa+yb|=1.
 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
数列{an}是公比为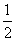 的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=nλ·bn+1(λ为常数,且λ≠1).
的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=nλ·bn+1(λ为常数,且λ≠1).
(1)求数列{an}的通项公式及λ的值;
(2)比较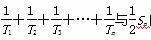 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知O为坐标原点,向量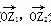 分别对应复数z1,z2,且z1=
分别对应复数z1,z2,且z1=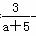 +(10-a2)i,z2=
+(10-a2)i,z2=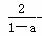 +(2a-5)i(a∈R),若
+(2a-5)i(a∈R),若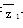 +z2是实数.
+z2是实数.
(1) 求实数a的值;
(2) 求以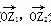 为邻边的平行四边形的面积.
为邻边的平行四边形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知向量a=(1,2),b=(-2,m),x=a+(t2+1)b,y=-ka+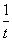 b,m∈R,k、t为正实数.
b,m∈R,k、t为正实数.
(1) 若a∥b,求m的值;
(2) 若a⊥b,求m的值;
(3) 当m=1时,若x⊥y,求k的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
设两个向量e1、e2满足|e1|=2,|e2|=1,e1、e2的夹角为60°,若向量2te1+7e2与向量e1+te2的夹角为钝角,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,正方体ABCD-A1B1C1D1中,E,F分别为棱AB,CC1的中点,在平面ADD1A1内且与平面D1EF平行的直线( )
A.有无数条 B.有2条
C.有1条 D.不存在

查看答案和解析>>
科目:高中数学 来源: 题型:
将函数y=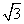 cos x+sin x(x∈R)的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( )
cos x+sin x(x∈R)的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( )
A. 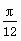 B.
B. 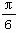
C.  D.
D. 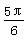
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com