
分析 (1)求出函数的导数,求得切线的斜率和切线方程,解方程可得N的坐标,再由焦点弦方程代入抛物线方程,即可得到定值t=-2;
(2)化简g(x),求出导数,并分解因式,对a讨论,当a≤0时,当0<a<2时,当a=2时,当a>2时,通过导数解不等式即可得到单调区间;
(3)构造函数h(x)=$\frac{ln{x}^{2}}{{x}^{2}}$(x>0),求出导数,判断单调性,可得最大值,再由累加法即可得证.
解答 (1)证明:抛物线方程y=$\frac{{x}^{2}}{8}$,求导得y′=$\frac{x}{4}$,
设切点A(x1,$\frac{{{x}_{1}}^{2}}{8}$),B(x2,$\frac{{{x}_{2}}^{2}}{8}$),
∴kNA=$\frac{{x}_{1}}{4}$,kNB═$\frac{{x}_{2}}{4}$,
∴切线NA的方程为:y-$\frac{{{x}_{1}}^{2}}{8}$=$\frac{{x}_{1}}{4}$(x-x1)即y=$\frac{{x}_{1}}{4}$x-$\frac{{{x}_{1}}^{2}}{8}$,
切线NB的方程为:y=$\frac{{x}_{2}}{4}$x-$\frac{{{x}_{2}}^{2}}{8}$,
联立直线NA,NB的方程,解得$\left\{\begin{array}{l}{x=\frac{{x}_{1}+{x}_{2}}{2}}\\{y=\frac{{x}_{1}{x}_{2}}{8}}\end{array}\right.$,
设焦点弦AB的方程为y=kx+2,代入抛物线方程可得,
x2-8kx-16=0,即有x1x2=-16,x1+x2=8k,
则有N(4k,-2),点N的纵坐标是一个定值t=-2;
(2)解:g(x)=8f(x)-(a-t)x+alnx=x2-(a+2)x+alnx,x>0.
g′(x)=2x-(a+2)+$\frac{a}{x}$=$\frac{(x-1)(2x-a)}{x}$,
当$\frac{a}{2}$=1,即a=2时,g′(x)≥0,g(x)在(0,+∞)递增;
当$\frac{a}{2}$>1,即a>2时,当x>$\frac{a}{2}$或0<x<1时,g′(x)>0,g(x)在(0,1),($\frac{a}{2}$,+∞)递增,
当1<x<$\frac{a}{2}$时,g′(x)<0,g(x)在(1,$\frac{a}{2}$)递减;
当a≤0时,易得g(x)在(0,1)递减,在(1,+∞)递增;
当0<a<2时,当x>1或0<x<$\frac{a}{2}$时,g′(x)>0,g(x)在(0,$\frac{a}{2}$),(1,+∞)递增,
当$\frac{a}{2}$<x<1时,g′(x)<0,g(x)在($\frac{a}{2}$,1)递减.
综上可得,当a≤0时,g(x)的增区间为(1,+∞),减区间为(0,1);
当0<a<2时,g(x)的增区间为(0,$\frac{a}{2}$),(1,+∞),减区间为($\frac{a}{2}$,1).
当a=2时,g(x)的增区间为(0,+∞);
当a>2时,g(x)的增区间为(0,1),($\frac{a}{2}$,+∞),g(x)的减区间为(1,$\frac{a}{2}$).
(3)证明:令h(x)=$\frac{ln{x}^{2}}{{x}^{2}}$(x>0),导数为h′(x)=$\frac{2(1-2lnx)}{{x}^{3}}$,
当0<x<$\sqrt{e}$时,h′(x)>0,h(x)在(0,$\sqrt{e}$)递增,
当x>$\sqrt{e}$时,h′(x)<0,h(x)在($\sqrt{e}$,+∞)递减.
即有h(x)在(0,+∞)的最大值为h($\sqrt{e}$)=$\frac{1}{e}$,
即有h(x)$≤\frac{1}{e}$,
则$\frac{ln{2}^{2}}{{2}^{2}}$+$\frac{ln{3}^{2}}{{3}^{2}}$+…+$\frac{ln{n}^{2}}{{n}^{2}}$≤$\frac{1}{e}$+$\frac{1}{e}$+…+$\frac{1}{e}$=$\frac{n-1}{e}$.
点评 本题考查导数的运用:求切线方程和单调区间和极值、最值,同时考查不等式的证明方法,注意构造函数运用单调性,同时考查分类讨论的思想方法,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-3,1) | B. | (-1,$\frac{1}{3}$) | C. | (-∞,-1)∪($\frac{1}{3}$,+∞) | D. | (-∞,-$\frac{1}{3}$)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知圆心为C的圆经过A(1,1)和B(2,-2),且圆心C在直线l:x-y+1=0上
已知圆心为C的圆经过A(1,1)和B(2,-2),且圆心C在直线l:x-y+1=0上查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设F为抛物线C:x2=2py(p>0)的焦点,点F到直线l:x+y+2=0的距离为$\frac{3}{2}\sqrt{2}$.
设F为抛物线C:x2=2py(p>0)的焦点,点F到直线l:x+y+2=0的距离为$\frac{3}{2}\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
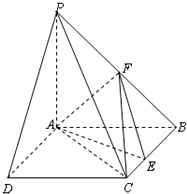 如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在边BC上移动.
如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在边BC上移动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com