
分析 根据题意,按数字1出现的位置分三种情况讨论,①、5个1都出现在i=j即a11、a22、a33、a44、a55这5个表格中,②、有1个1出现在a11、a22、a33、a44、a55这5个表格中,剩余4个1在其他位置,③、有3个1出现在a11、a22、a33、a44、a55这5个表格中,剩余2个1在其他位置,分别求出每种情况下填表方法的数目,进而由分类计数原理计算可得答案.
解答 解:根据题意,在5×5的表格中,有5个i=j的表格,即a11、a22、a33、a44、a55,10个i>j的表格,10个i<j的表格;
要求5×5的表格种恰有5个1,则对1出现的位置分3种情况讨论:
①、5个1都出现在i=j即a11、a22、a33、a44、a55这5个表格中,有1种情况;
②、有1个1出现在a11、a22、a33、a44、a55这5个表格中,剩余4个1在其他位置,
需要先在a11、a22、a33、a44、a55这5个表格中,选出1个,有C51种情况,
在剩下的10个aij(i>j)表格中,任选2个,有C102种情况,
则有C51×C102=225种填表方法;
③、有3个1出现在a11、a22、a33、a44、a55这5个表格中,剩余2个1在其他位置,
需要先在a11、a22、a33、a44、a55这5个表格中,选出3个,有C53种情况,
在剩下的10个aij(i>j)表格中,任选1个,有C101种情况,
则有C53×C101=100种填表方法;
则一共有1+225+100=326种填表方法;
故答案为:326.
点评 本题考查排列组合的应用,关键是正确理解题意的要求,进而进行分类讨论.


 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{π}{45}$ | D. | $\frac{45-π}{45}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1或2 | B. | $\sqrt{2}$或2 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
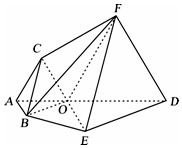 如图,ABEDEFC为多面体,平面ABED⊥平面ACED,点O在线段AD上,OA=1,OD=2,△OAB,△OAC,△ODE,△ODF都是正三角形.
如图,ABEDEFC为多面体,平面ABED⊥平面ACED,点O在线段AD上,OA=1,OD=2,△OAB,△OAC,△ODE,△ODF都是正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 7 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45° | B. | 30° | C. | 15° | D. | 60° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com