
分析 (Ⅰ)设数列{an}的首项为a1,公差为d;从而可得a5=a1+4d=0,a1=2(2a1+d)+8,从而解得;
(Ⅱ)分类讨论,从而化简可得$\frac{{a}_{n}}{{a}_{n-1}}$=3,从而证明并求和.
解答 解:(Ⅰ)设数列{an}的首项为a1,公差为d;
则a5=a1+4d=0,a1=2(2a1+d)+8,
解得,a1=-$\frac{16}{5}$,d=$\frac{4}{5}$;
故an=-$\frac{16}{5}$+(n-1)$\frac{4}{5}$=$\frac{4}{5}$n-4;
(Ⅱ)证明:∵2Sn=3an-1,
①当n=1时,2S1=3a1-1,
解得,a1=1,
②当n≥2时,2Sn=3an-1,2Sn-1=3an-1-1,
故2an=3an-3an-1,
故$\frac{{a}_{n}}{{a}_{n-1}}$=3,
故数列{an}是以1为首项,3为公比的等比数列,
故Sn=$\frac{1-{3}^{n}}{1-3}$=$\frac{1}{2}$(3n-1).
点评 本题考查了等差数列与等比数列的应用及分类讨论的思想应用,同时考查了方程思想的应用.


科目:高中数学 来源: 题型:选择题
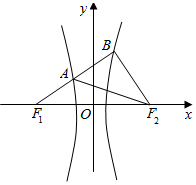 已知F1,F2分别为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点,若存在过F1的直线分别交双曲线C的左、右支于A,B两点,使得∠BAF2=∠BF2F1,则双曲线C的离心率e的取值范围是( )
已知F1,F2分别为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点,若存在过F1的直线分别交双曲线C的左、右支于A,B两点,使得∠BAF2=∠BF2F1,则双曲线C的离心率e的取值范围是( )| A. | (3,+∞) | B. | (1,2+$\sqrt{5}$) | C. | (3,2+$\sqrt{5}$) | D. | (1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,3] | B. | [1,3] | C. | [-1,11] | D. | [-5,11] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题p是真命题 | B. | 命题p的逆命题是真命题 | ||
| C. | 命题p的否命题是:若a<1,则a2≥1 | D. | 命题p的逆否命题是:若a2≥1,则a<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
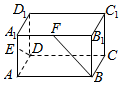 如图所示的长方体中,$AB=2\sqrt{6},AD=\sqrt{5},C{C_1}=2\sqrt{3},E,F$分别为AA1,A1B1的中点,则异面直线DE,BF所成角的大小为( )
如图所示的长方体中,$AB=2\sqrt{6},AD=\sqrt{5},C{C_1}=2\sqrt{3},E,F$分别为AA1,A1B1的中点,则异面直线DE,BF所成角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com