
分析 由题意可得p,q真时,a的范围,分别由p真q假,p假q真由集合的运算可得.
解答 解:∵命题p:不等式x2-(a+1)x+1>0的解集是R
∴△=(a+1)2-4<0,解得-3<a<1,
∵命题q:函数f(x)=(a+1)x在定义域内是增函数.
∴a+1>1,解得a>0
由p∧q为假命题,p∨q为真命题,可知p,q一真一假,
当p真q假时,由{a|-3<a<1}∩{a|a≤0}={a|-3<a≤0}
当p假q真时,由{a|a≤-3,或a≥1}∩{a|a>0}={a|a≥1}
综上可知a的取值范围为:{a|-3<a≤0,或a≥1}
点评 本题考查复合命题的真假,涉及一元二次不等式的解法和指数函数的单调性,属基础题.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:选择题
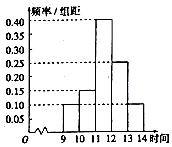 一商场在某日促销活动中,对9时至14时的销售额进行统计,其频率分布直方图如图所示,已知9时至10时的销售额为2.5万元,则11时至12时的销售为( )
一商场在某日促销活动中,对9时至14时的销售额进行统计,其频率分布直方图如图所示,已知9时至10时的销售额为2.5万元,则11时至12时的销售为( )| A. | 100万元 | B. | 10万元 | C. | 7.5万元 | D. | 6.25万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com