
| A. | (-$\frac{π}{12}$,0) | B. | (-$\frac{π}{12}$,$\frac{5}{4}$) | C. | (-$\frac{5π}{12}$,0) | D. | ($\frac{5}{6}$π,$\frac{5}{4}$) |
分析 利用数量积公式得出f(x)解析式,利用三角恒等变换化简,根据正弦函数的性质求出A,ω,得出对称中心.
解答 解:f(x)=1+Acos2ωx+$\sqrt{3}$Acosωxsinωx=1+$\frac{A}{2}$(1+cos2ωx)+$\frac{\sqrt{3}}{2}$Asin2ωx=1+$\frac{A}{2}$+Asin(2ωx+$\frac{π}{6}$),
∵单调区间[m,n]的最大长度为$\frac{π}{2}$,
∴f(x)的周期T=π,即$\frac{2π}{2ω}$=π,∴ω=1.
∵函数f(x)的图象在y轴上的截距为$\frac{3}{2}$,即f(0)=$\frac{3}{2}$,∴1+$\frac{A}{2}$+$\frac{A}{2}$=$\frac{3}{2}$,∴A=$\frac{1}{2}$,
∴f(x)=$\frac{5}{4}$+$\frac{1}{2}$sin(2x+$\frac{π}{6}$),
令2x+$\frac{π}{6}$=kπ得x=-$\frac{π}{12}$+$\frac{kπ}{2}$,k∈Z.
∴当k=0时,(-$\frac{π}{12}$,$\frac{5}{4}$)为f(x)的一个对称中心,
故选:B.
点评 本题考查了平面向量的数量积,三角恒等变换与正弦函数的图象与性质,属于中档题.


科目:高中数学 来源: 题型:解答题
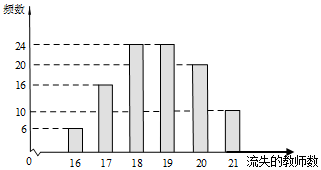 2017年两会继续关注了乡村教师的问题,随着城乡发展失衡,乡村教师待遇得不到保障,流失现象严重,教师短缺会严重影响乡村孩子的教育问题,为此,某市今年要为某所乡村中学招聘储备未来三年的教师,现在每招聘一名教师需要2万元,若三年后教师严重短缺时再招聘,由于各种因素,则每招聘一名教师需要5万元,已知现在该乡村中学无多余教师,为决策应招聘多少乡村教师搜集并整理了该市100所乡村中学在过去三年内的教师流失数,得到右面的柱状图:记x表示一所乡村中学在过去三年内流失的教师数,y表示一所乡村中学未来四年内在招聘教师上所需的费用(单位:万元),n表示今年为该乡村中学招聘的教师数,为保障乡村孩子教育不受影响,若未来三年内教师有短缺,则第四年马上招聘
2017年两会继续关注了乡村教师的问题,随着城乡发展失衡,乡村教师待遇得不到保障,流失现象严重,教师短缺会严重影响乡村孩子的教育问题,为此,某市今年要为某所乡村中学招聘储备未来三年的教师,现在每招聘一名教师需要2万元,若三年后教师严重短缺时再招聘,由于各种因素,则每招聘一名教师需要5万元,已知现在该乡村中学无多余教师,为决策应招聘多少乡村教师搜集并整理了该市100所乡村中学在过去三年内的教师流失数,得到右面的柱状图:记x表示一所乡村中学在过去三年内流失的教师数,y表示一所乡村中学未来四年内在招聘教师上所需的费用(单位:万元),n表示今年为该乡村中学招聘的教师数,为保障乡村孩子教育不受影响,若未来三年内教师有短缺,则第四年马上招聘查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. | 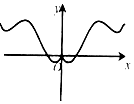 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com