
分析 由题意可证A1O⊥BD,OF⊥BD,利用线面垂直的判定可证BD⊥平面A1OF,进而利用线面垂直的性质即可证明得解.
解答 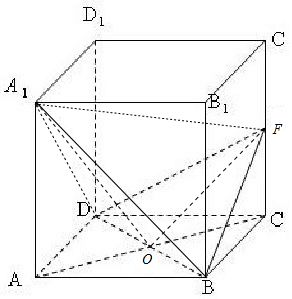 解:如图,连接,A1O,A1F,OF,
解:如图,连接,A1O,A1F,OF,
∵在正方体ABCD-A1B1C1D1中,A1D=A1B,O为BD的中点,
∴A1O⊥BD,
又∵F是CC1的中点,可得:DF=BF,
∴OF⊥BD,
又∵A1O∩OF=O,
∴BD⊥平面A1OF,
∵A1F?平面A1OF,
∴BD⊥A1F.
点评 本题主要考查了线面垂直的性质,要证线线垂直,可找线面垂直,反之亦然.这是立体几何证明垂直时常用的转化方法.除此之外,也要注意有时是从数量关系通过计算找线线垂直,如勾股定理等,有时会利用平面几何的性质,如等腰三角形底边上的三线合一等等,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
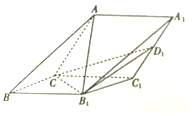 如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2$\sqrt{3}$.
如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
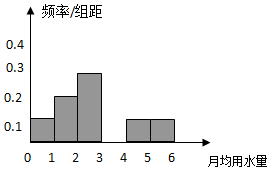 某市为了节约生活用水,计划在本市试行居民生活用水定额管理.为了较合理地确定居民日常用水量的标准,有关部门抽样调查了100位居民.表是这100位居民月均用水量(单位:吨)的频率分布表,根据表解答下列问题:
某市为了节约生活用水,计划在本市试行居民生活用水定额管理.为了较合理地确定居民日常用水量的标准,有关部门抽样调查了100位居民.表是这100位居民月均用水量(单位:吨)的频率分布表,根据表解答下列问题:| 分组 | 频数 | 频率 |
| [0,1) | 10 | 0.1 |
| [1,2) | a | 0.2 |
| [2,3) | 30 | 0.3 |
| [3,4) | 20 | b |
| [4,5) | 10 | 0.1 |
| [5,6) | 10 | 0.1 |
| 合计 | 100 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 明天该地区约有80%的时间会下雨,20%的时间不下雨 | |
| B. | 明天该地区约有80%的地方会下雨,20%的地方不下雨 | |
| C. | 明天该地区下雨的可能性为80% | |
| D. | 该地区约有80%的人认为明天会下雨,20%的人认为明天不下雨 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4x+3y-7=0 | B. | 3x+4y+1=0 | C. | 3x-4y-7=0 | D. | 4y-3x-1=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com