
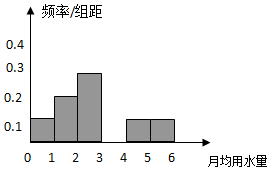
 某市为了节约生活用水,计划在本市试行居民生活用水定额管理.为了较合理地确定居民日常用水量的标准,有关部门抽样调查了100位居民.表是这100位居民月均用水量(单位:吨)的频率分布表,根据表解答下列问题:
某市为了节约生活用水,计划在本市试行居民生活用水定额管理.为了较合理地确定居民日常用水量的标准,有关部门抽样调查了100位居民.表是这100位居民月均用水量(单位:吨)的频率分布表,根据表解答下列问题:| 分组 | 频数 | 频率 |
| [0,1) | 10 | 0.1 |
| [1,2) | a | 0.2 |
| [2,3) | 30 | 0.3 |
| [3,4) | 20 | b |
| [4,5) | 10 | 0.1 |
| [5,6) | 10 | 0.1 |
| 合计 | 100 | 1 |
分析 (1)由频率分布表,根据频率与频数的关系,即可求出a、b的值;
(2)根据第4组的频率,补充完整频率分布直方图,
根据直方图中小矩形最高的是第三组,估计该市每位居民月均用水量众数.
解答 解:(1)由频率分布表得出第二小组的频率为:0.02,故a=100×0.2=20;
由频率分布表得出第四组的频数为20,频率为b=$\frac{20}{100}$=0.2;
(2)第4组的频率为0.2,补充完整频率分布直方图,如图所示; 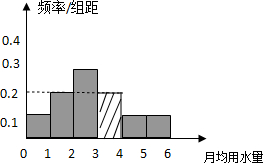
根据直方图,小矩形最高的是第三组,
估计该市每位居民月均用水量的众数为$\frac{2+3}{2}$=2.5.
点评 本题考查了用样本估计总体,以及频率分布直方图的应用问题,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | y=±$\frac{\sqrt{3}}{3}$x | B. | y=±$\sqrt{3}$x | C. | y=±2x | D. | y=±$\sqrt{5}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{-7-i}{5}$ | B. | $\frac{-7+i}{5}$ | C. | $\frac{7+i}{5}$ | D. | $\frac{7-i}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com