
分析 (1)由题意可得f′(2)=0,f(2)=-$\frac{4}{3}$,由此列方程组可解得a,b,从而可得f(x)解析式;
(2)由(1)所求解析式可得f′(x),利用导数可得f(x)的单调区间及极值,根据f(x)的图象的大致形状即可求得k的范围;
解答 解:(1)函数f(x)=ax3-bx+4(a,b∈R),可得f′(x)=3ax2-b,
依题意得$\left\{\begin{array}{l}{f′(2)=12a-b=0}\\{f(2)=8a-2b+4=-\frac{4}{3}}\end{array}\right.$,解得a=$\frac{1}{3}$,b=4,
所以所求解析式为f(x)=$\frac{1}{3}$x3-4x+4.
(2)由(1)可得f′(x)=x2-4=(x+2)(x-2),
令f′(x)=0,得x=±2,
当x<-2或x>2时f′(x)>0,当-2<x<2时,f′(x)<0;
所以当x=-2时f(x)取得极大值,f(-2)=$\frac{8}{3}$,当x=2时f(x)取得极小值,f(2)=-$\frac{4}{3}$,
要使方程f(x)=k有3个解,只需-$\frac{4}{3}$<k<$\frac{8}{3}$.
故实数k的取值范围为:-$\frac{4}{3}$<k<$\frac{8}{3}$.
点评 本题考查函数在某点取得极值的条件及根的个数判断,考查数形结合思想,属中档题.


科目:高中数学 来源: 题型:解答题
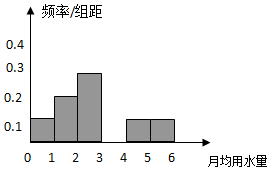 某市为了节约生活用水,计划在本市试行居民生活用水定额管理.为了较合理地确定居民日常用水量的标准,有关部门抽样调查了100位居民.表是这100位居民月均用水量(单位:吨)的频率分布表,根据表解答下列问题:
某市为了节约生活用水,计划在本市试行居民生活用水定额管理.为了较合理地确定居民日常用水量的标准,有关部门抽样调查了100位居民.表是这100位居民月均用水量(单位:吨)的频率分布表,根据表解答下列问题:| 分组 | 频数 | 频率 |
| [0,1) | 10 | 0.1 |
| [1,2) | a | 0.2 |
| [2,3) | 30 | 0.3 |
| [3,4) | 20 | b |
| [4,5) | 10 | 0.1 |
| [5,6) | 10 | 0.1 |
| 合计 | 100 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
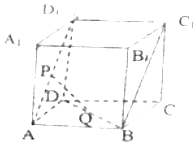 如图,点P、Q分别是正方体ABCD-A1B1C1D1的面对角线AD1、BD的中点,则异面直线PQ和BC1所成的角为( )
如图,点P、Q分别是正方体ABCD-A1B1C1D1的面对角线AD1、BD的中点,则异面直线PQ和BC1所成的角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4x+3y-7=0 | B. | 3x+4y+1=0 | C. | 3x-4y-7=0 | D. | 4y-3x-1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{2016}$ | D. | 2016 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
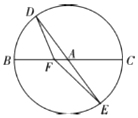 如图,BC是单位圆A的一条直径,F是线段AB上的点,且$\overrightarrow{BF}$=3$\overrightarrow{FA}$,若DE是圆A中绕圆心A运动的一条直径,则$\overrightarrow{FD}$•$\overrightarrow{FE}$的值是$-\frac{15}{16}$.
如图,BC是单位圆A的一条直径,F是线段AB上的点,且$\overrightarrow{BF}$=3$\overrightarrow{FA}$,若DE是圆A中绕圆心A运动的一条直径,则$\overrightarrow{FD}$•$\overrightarrow{FE}$的值是$-\frac{15}{16}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com