
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
分析 由题意可得O为△ABC的外心,也是BC的中点,∠A=$\frac{π}{2}$,设AC=1,则BC=2,由此求得∠B的值,可得$\overrightarrow{AB}$与$\overrightarrow{BC}$的夹角的值.
解答 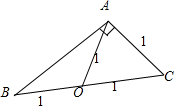 解:∵点O为△ABC所在平面内一点,${\overrightarrow{OA}^2}={\overrightarrow{OB}^2}={\overrightarrow{OC}^2}$,
解:∵点O为△ABC所在平面内一点,${\overrightarrow{OA}^2}={\overrightarrow{OB}^2}={\overrightarrow{OC}^2}$,
∴O为△ABC的外心,
若$\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AO}$,则O也是BC的中点,
∴△ABC为直角三角形,∠A=$\frac{π}{2}$,
∵$|{\overrightarrow{AC}}|=|{\overrightarrow{AO}}|$,设AC=1,则BC=2,∴AB=$\sqrt{{BC}^{2}{-AC}^{2}}$=$\sqrt{3}$,
∴$\overrightarrow{AB}$与$\overrightarrow{BC}$的夹角为π-∠B=π-$\frac{π}{6}$=$\frac{5π}{6}$,
故选:D.
点评 本题主要考查两个向量的加减法的法则,以及其几何意义,求两个向量的夹角,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{-7-i}{5}$ | B. | $\frac{-7+i}{5}$ | C. | $\frac{7+i}{5}$ | D. | $\frac{7-i}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
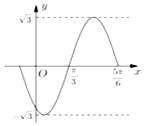 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π),x∈R的部分图象,则下列命题中,正确的命题序号是( )
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π),x∈R的部分图象,则下列命题中,正确的命题序号是( )| A. | ③⑤ | B. | ③④ | C. | ④⑤ | D. | ①③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 明天本地有80%的时间下雨,20%的时间不下雨 | |
| B. | 明天本地有80%的区域下雨,20%的区域不下雨 | |
| C. | 明天本地下雨的机会是80% | |
| D. | 气象局并没有对明天是否下雨作出有意义的预报 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com