
分析 利用集合S具有性质P的概念,{-5,5}-5,5与{-2,1,2,4}分析判断即可;
取A1(xi,xi),集合S具有性质P,故存在点A2(xi,xj)使得OA1⊥OA2,利用向量的坐标运算整理即可证得xi+xj=0;数列{xn}中一定存在两项xi,xj使得xi+xj=0;
解答 解:集合S具有性质P,若A1(-5,5),则A2(5,5),若A1(-5,-5)则A2(5,-5),均满足OA1⊥OA2,所以①具有性质P,故①正确;
对于②,当A1(-2,3)若存在A2(x,y)满足OA1⊥OA2,即-2x+3y=0,即$\frac{y}{x}=\frac{2}{3}$,集合S中不存在这样的数x,y,因此②不具有性质P,故②不正确;
取A1(xi,xi),又集合S具有性质P,所以存在点A2(xi,xj)使得OA1⊥OA2,即xixi+xixj=0,又xi≠0,所以xi+xj=0,故③正确;
由③知,集合S中一定存在两项xi,xj使得xi+xj=0;
假设x2≠1,则存在k(2<k<n,k∈N*)有xk=1,所以0<x2<1.
此时取A1(x2,xn),集合S具有性质P,所以存在点A2(xi,xs)使得OA1⊥OA2,
所以x2xi+xnxs=0;只有x1,所以当x1=-1时x2=xnxs>xs≥x2,矛盾,∴xi是S中任一数,则在S中一定存在xj,使得xi+xj=0.故④不正确;
故答案为:①③
点评 考查新概念的理解与应用,突出考查抽象思维与反证法的综合应用,属于难题.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:选择题
| A. | x=-$\frac{π}{6}$ | B. | x=$\frac{π}{12}$ | C. | x=-$\frac{π}{12}$ | D. | x=$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{3}$ | B. | -$\frac{3}{4}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{y^2}{3}-\frac{x^2}{4}=1$ | B. | $\frac{y^2}{4}-\frac{x^2}{3}=1$ | C. | $\frac{x^2}{3}-\frac{y^2}{4}=1$ | D. | $\frac{x^2}{4}-\frac{y^2}{3}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
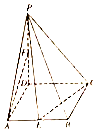 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=4,点E、F分别为AB和PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=4,点E、F分别为AB和PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com