
已知二次函数f(x)有两个零点0和-2,且f(x)最小值是-1,函数g(x)与f(x)的图象关于原点对称.
(1)求f(x)和g(x)的解析式;
(2)若h(x)=f(x)-λg(x)在区间[-1,1]上是增函数,求实数λ的取值范围.
解析:(1)依题意,设f(x)=ax(x+2)=ax2+2ax(a>0).
∵f(x)图象的对称轴是x=-1,
∴f(-1)=-1,即a-2a=-1,得a=1.
∴f(x)=x2+2x.
又∵函数g(x)的图象与f(x)的图象关于原点对称,
∴g(x)=-f(-x)=-x2+2x.
(2)由(1)得h(x)=x2+2x-λ(-x2+2x)
=(λ+1)x2+2(1-λ)x.
①当λ=-1时,h(x)=4x满足在区间[-1,1]上是增函数;
②当λ<-1时,h(x)图象对称轴是x=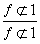 ,
,
则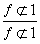 ≥1,又λ<-1,解得λ<-1;
≥1,又λ<-1,解得λ<-1;
③当λ>-1时,同理则需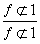 ≤-1,
≤-1,
又λ>-1,解得-1<λ≤0.
综上,满足条件的实数λ的取值范围是(-∞,0].


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com