
分析 (1)由f(-x)=-f(x),得:$sin({-x+\frac{π}{3}})=-sin({x+\frac{π}{3}})$,解得${x_0}=\frac{π}{2}∈R$,可得结论;
(2)若f(x)=2x+m是定义在[-1,1]上的“M类函数”,则存在实数x0∈[-1,1]满足f(-x0)=-f(x0),即方程2x+2-x+2m=0在[-1,1]上有解,进而可得实数m的最小值;
(3)若f(x)=$\left\{\begin{array}{l}{log_2}({x^2}-2mx)\\-3\end{array}\right.\begin{array}{l}{,\;\;x≥2}\\{,\;\;x<2}\end{array}$为其定义域上的“M类函数”,则存在实数x0,满足f(-x0)=-f(x0),进而可得实数m的取值范围.
解答 解:(1)由f(-x)=-f(x),得:$sin({-x+\frac{π}{3}})=-sin({x+\frac{π}{3}})$…(1分)
所以$\sqrt{3}cosx=0$…(3分)
所以存在${x_0}=\frac{π}{2}∈R$满足f(-x0)=-f(x0)
所以函数$f(x)=sin({x+\frac{π}{3}})$是“M类函数”…(4分)
(2)因为f(x)=2x+m是定义在[-1,1]上的“M类函数”,
所以存在实数x0∈[-1,1]满足f(-x0)=-f(x0),
即方程2x+2-x+2m=0在[-1,1]上有解,…(5分)
令$t={2^x}∈[{\frac{1}{2},2}]$…(6分)
则$m=-\frac{1}{2}(t+\frac{1}{t})$
因为$g(t)=-\frac{1}{2}(t+\frac{1}{t})$在$[\frac{1}{2},1]$上递增,在[1,2]上递减…(8分)
所以当$t=\frac{1}{2}$或t=2时,m取最小值$-\frac{5}{4}$…(9分)
(3)由x2-2mx>0对x≥2恒成立,得m<1…(10分)
因为若$f(x)=\left\{\begin{array}{l}{log_2}({x^2}-2mx)\\-3\end{array}\right.\begin{array}{l}{,\;\;x≥2}\\{,\;\;x<2}\end{array}$为其定义域上的“M类函数”
所以存在实数x0,满足f(-x0)=-f(x0)
①当x0≥2时,-x0≤-2,
所以$-3=-{log_2}({x_0}^2-2m{x_0})$,所以$m=\frac{1}{2}{x_0}-\frac{4}{x_0}$
因为函数$y=\frac{1}{2}x-\frac{4}{x}(x≥2)$是增函数,所以m≥-1…(12分)
②当-2<x0<2时,-2<-x0<2,所以-3=3,矛盾…(13分)
③当x0≤-2时,-x0≥2,所以${log_2}({x_0}^2+2m{x_0})=3$,所以$m=-\frac{1}{2}{x_0}+\frac{4}{x_0}$
因为函数$y=-\frac{1}{2}x+\frac{4}{x}(x≤-2)$是减函数,所以m≥-1…(15分)
综上所述,实数m的取值范围是[-1,1)…(16分)
点评 本题考查的知识点是分段函数的定义,新定义“M类函数”,正确理解新定义“M类函数”的含义,是解答的关键.


科目:高中数学 来源: 题型:选择题
| A. | 4i | B. | -4i | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
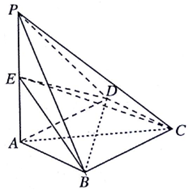 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,PA=AB=2,E为PA的中点,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,PA=AB=2,E为PA的中点,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com