Question

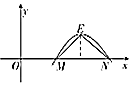
4．已知奇函数f（x）=Acos（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的导函数的部分图象如图所示，E是最高点，且△MNE是边长为1的正三角形，那么$f（{\frac{1}{3}}）$=（　　）

• A． $-\frac{{\sqrt{3}}}{2π}$
• B． $-\frac{1}{2}$
• C． $\frac{1}{4}$
• D． $-\frac{3}{4π}$

Answer 1

分析 首先由已知函数为奇函数求出φ，然后结合图象求出函数的周期以及最值，得到函数解析式，然后求$f（{\frac{1}{3}}）$．

解答 解：由已知函数为奇函数得到f（0）=Acosφ=0，得到φ=$\frac{π}{2}$，又由函数f（x）=Acos（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的导函数f'（x）=-Aωsin（ωx+φ）的部分图象得到T=2，所以ω=π，并且Aω=$\frac{\sqrt{3}}{2}$，所以A=$\frac{\sqrt{3}}{2π}$，所以f（x）=$\frac{\sqrt{3}}{2π}$cos（πx+$\frac{π}{2}$）=$-\frac{\sqrt{3}}{2π}sin（πx）$，所以$f（{\frac{1}{3}}）$=$-\frac{\sqrt{3}}{2π}sin\frac{π}{3}=-\frac{3}{4π}$；
故选：D．

点评 本题考查了三角函数的图象以及性质；熟练掌握正弦函数的图象是解答此类题目的关键．