
分析 由题意和等差数列的通项公式得a1+53d=4028,由d为正整数得a1是53的倍数,由等比中项的性质列出式子:a542=a1ak=4×4×19×19×53×53,对a1分类讨论,分别化简后结合题意可得结论.
解答 解:由题意得a54=4028,则a1+53d=4028,
化简得$\frac{{a}_{1}}{53}$+d=76,
∵d为正整数,∴a1是53的倍数,
∵a1,a54,ak成等比数列,
∴a542=a1ak=4×4×19×19×53×53,且an是整数,
(1)若a1=53,53+53d=4028,解得d=75,
此时ak=4×4×19×19×53=53+75(k-1),得k=4081,成立,
(2)若a1=2×53,106+53d=4028,解得d=74,
此时ak=2×4×19×19×53=2×53+74(k-1),得k=2886,成立,
(3)若a1=3×53,159+53d=4028,解得d=73,
此时ak=$\frac{1}{3}$(4×4×19×19×53)不是整数,舍去,
(3)若a1=4×53,212+53d=4028,解得d=72,
此时ak=4×19×19×53=4×53+72(k-1),得k=1060,成立,
(4)若a1=16×53=848,848+53d=4028,得53d=3180,d=60,
此时ak=19×19×53=16×53+60(k-1),得k不是整数,不成立,
(5)若a1=19×53=1007,1007+53d=4028,得53d=3021,d=57,
此时ak=4×4×19×53=19×53+57(k-1),得k=265,成立,
(6)若a1=53×53=2809,2809+53d=4028,得53d=1219,d=23,
此时ak=4×4×19×19=53×53+72(k-1),得k=129,成立,
∴公差d的所有可能取值之和为75+74+72+57+23=301.
故答案为:301.
点评 本题考查等差数列的通项公式,等比中项的性质,考查分类讨论的数学思想、以及化简、计算能力,确定a1是53的倍数是关键.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{2014}{2015}$ | B. | $\frac{2015}{2016}$ | C. | $\frac{2016}{2017}$ | D. | $\frac{2017}{2018}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,4} | B. | {-2,4} | C. | {-2,2,4} | D. | {-4,2,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
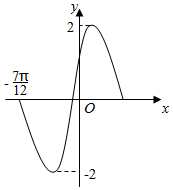 已知函数y=Asin(ωx+φ),(A>0,ω>0,|φ|<π)的图象如图所示,则该函数的解析式是y=2sin(2x+$\frac{π}{6}$).
已知函数y=Asin(ωx+φ),(A>0,ω>0,|φ|<π)的图象如图所示,则该函数的解析式是y=2sin(2x+$\frac{π}{6}$).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{4}$个长度单位 | B. | 向右平移$\frac{π}{4}$个长度单位 | ||
| C. | 向左平移$\frac{π}{2}$个长度单位 | D. | 向右平移$\frac{π}{2}$个长度单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | (0,3) | C. | (-1,1) | D. | (-1,0] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com