
分析 (Ⅰ)由二倍角公式及辅助角公式将f(x)化简,由正弦函数周期公式,代入求得ω值,求得f(x)的解析式,根据x的取值范围,即可求得y=f(x)的值域;
(Ⅱ)f($\frac{A}{2}$)=1,由A∈(0,π)求得$A=\frac{2π}{3}$,由余弦定理求得bc=9,再由三角形面积公式,S=$\frac{1}{2}$bcsinA,即可求得△ABC的面积.
解答 解:(Ⅰ)$f(x)={cos^2}ωx+\sqrt{3}sinωxcosωx$,
=$\frac{1}{2}(1+cos2ωx)+\frac{{\sqrt{3}}}{2}sin2ωx$,
=$sin({2ωx+\frac{π}{6}})+\frac{1}{2}$.(3分)
因为T=π,ω>0,
所以$\frac{2π}{2ω}=π$,ω=1.
所以$f(x)=sin({2x+\frac{π}{6}})+\frac{1}{2}$,
又$0≤x≤\frac{π}{2}$,
所以$\frac{π}{6}≤2x+\frac{π}{6}≤\frac{7π}{6}$,
所以$-\frac{1}{2}≤sin(2x+\frac{π}{6})≤1$,
所以$0≤sin({2x+\frac{π}{6}})+\frac{1}{2}≤\frac{3}{2}$,
当$x∈[{0,\frac{π}{2}}]$时,函数f(x)的值域为$[{0,\frac{3}{2}}]$.(6分)
(Ⅱ)因为$f({\frac{A}{2}})=1$,
所以$sin({A+\frac{π}{6}})+\frac{1}{2}=1$,即$sin({A+\frac{π}{6}})=\frac{1}{2}$,
由A∈(0,π)知$\frac{π}{6}<A+\frac{π}{6}<\frac{7π}{6}$,
所以$A+\frac{π}{6}=\frac{5π}{6}$,
所以$A=\frac{2π}{3}$.(9分)
由余弦定理a2=b2+c2-2bccosA,即16=b2+c2+bc,
所以16=(b+c)2-bc,
因为b+c=5,所以bc=9,
所以${S_{△ABC}}=\frac{1}{2}bcsinA=\frac{1}{2}×9×sin\frac{2π}{3}=\frac{9}{4}\sqrt{3}$,
∴△ABC的面积$\frac{9\sqrt{3}}{4}$.(12分)
点评 本题考查三角恒等变换公式,正弦函数图象及性质,正弦定理及余弦定理的应用,三角形的面积公式,考查计算能力,属于中档题.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 4x | C. | 4+2d | D. | 4+2d2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
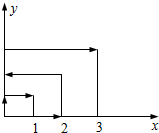 如图:一个质点在第一象限运动,在第一秒钟它由原点运动到点(0,1),而后接着按图所示在与x轴y轴平行的方向运动,且每秒移动一个单位长度,那么416秒后,这个质点所处的位置的坐标是(20,16).
如图:一个质点在第一象限运动,在第一秒钟它由原点运动到点(0,1),而后接着按图所示在与x轴y轴平行的方向运动,且每秒移动一个单位长度,那么416秒后,这个质点所处的位置的坐标是(20,16).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 5 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
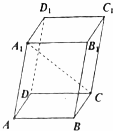 如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD是矩形,AB=4,AD=3,AA1=5,∠BAA1=∠DAA1=60°,则A1C的长为$\sqrt{85}$.
如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD是矩形,AB=4,AD=3,AA1=5,∠BAA1=∠DAA1=60°,则A1C的长为$\sqrt{85}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com