
| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
分析 逐个验证:①向量要考虑方向.
②利用等体积,即可判断;
③数集有些性质以传递的,但有些性质不能传递,因此,要判断类比的结果是否正确,关键是要在新的数集里进行论证,当然要想证明一个结论是错误的,也可直接举一个反例;
④在类比等差数列的性质推理等比数列的性质时,我们一般的思路有:由加法类比推理为乘法,由减法类比推理为除法,由算术平均数类比推理为几何平均数等.
解答 解:①由若a,b,c∈R则(ab)c=a(bc);类比推出:若$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$为三个向量则($\overrightarrow{a}$$\overrightarrow{b}$)$\overrightarrow{c}$=$\overrightarrow{a}$($\overrightarrow{b}$$\overrightarrow{c}$),不正确,因为($\overrightarrow{a}$•$\overrightarrow{b}$)•$\overrightarrow{c}$与$\overrightarrow{c}$共线,$\overrightarrow{a}$•($\overrightarrow{b}$•$\overrightarrow{c}$)与$\overrightarrow{a}$共线,当$\overrightarrow{a}$、$\overrightarrow{c}$方向不同时,向量的数量积运算结合律不成立;
②在正三角形ABC中,若D是边BC的中点,G是三角形ABC的重心,则$\frac{AG}{GD}$=2;类比推出:在棱长都相等的四面体ABCD中,若△BCD的中心为M,四面体内部一点O到四面体各面的距离都相等,则$\frac{AO}{OM}$=3,正确.
③在复数集C中,若z1,z2∈C,z12+z22=0,则可能z1=1且z2=i.故错误
④在类比等差数列的性质推理等比数列的性质时,我们一般的思路有:由加法类比推理为乘法,由减法类比推理为除法,由算术平均数类比推理为几何平均数等,故我们可以类比推出:若数列{cn}是各项都为正数的等比数列,dn=$\root{n}{{{c_1}•{c_2}•{c_3}•…•{c_n}}}$,则数列{dn}也是等比数列.正确.
故选:C.
点评 类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).但类比推理的结论不一定正确,还需要经过证明.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (-1,0) | B. | (1,1) | C. | (cos37°,sin37°) | D. | $\frac{\overline a}{{|{\overline a}|}}(|{\overline a}|≠0)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平行移动$\frac{π}{3}$个单位 | B. | 向左平行移动$\frac{π}{6}$个单位 | ||
| C. | 向右平行移动$\frac{π}{3}$个单位 | D. | 向右平行移动$\frac{π}{6}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p2+q2+r2+pq+qr+rp=d2 | B. | p3+q3+r3=d3 | ||
| C. | p2+q2+r2=d2 | D. | p+q+r=d |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ①③ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
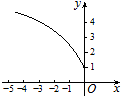 函数f(x)的图象如图所示,f′(x)是f(x)的导函数,设a=f′(-2),b=f′(-3),c=f(-2)-f(-3),则a,b,c由小到大的关系为a<c<b.
函数f(x)的图象如图所示,f′(x)是f(x)的导函数,设a=f′(-2),b=f′(-3),c=f(-2)-f(-3),则a,b,c由小到大的关系为a<c<b.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com