
分析 (Ⅰ)通过代入计算可知当n≥2时an=$\frac{1}{2}$,进而验证当n=1时是否成立即可;
(Ⅱ)一方面通过假设存在实数m使得数列{an}是等比数列,利用等比中项代入计算可知m=$\frac{1}{2}$,另一方面可知当m=$\frac{1}{2}$时an=$\frac{1}{2}$;
(Ⅲ)通过变形可知an+an+1=$\frac{{a}_{n+1}}{{a}_{n}}$,利用累乘法可知$\underset{\stackrel{n}{π}}{i=1}$(ai+1+ai)=$\frac{{a}_{n+1}}{m}$,通过构造函数y=2x2+x-1=2$(x+\frac{1}{4})^{2}$-$\frac{9}{8}$,利用单调性可知当0<x<$\frac{1}{2}$时y<0,从而可知当0<m<$\frac{1}{2}$时0<an+1<$\frac{1}{2}$,代入计算即得结论.
解答 (Ⅰ)解:依题意,a1=m=-1,
a2=f(a1)=$\frac{1}{1+1}$=$\frac{1}{2}$,
a3=f(a2)=$\frac{\frac{1}{{2}^{2}}}{1-\frac{1}{2}}$=$\frac{1}{2}$,
∴an=$\left\{\begin{array}{l}{-1,}&{n=1}\\{\frac{1}{2},}&{n≥2}\end{array}\right.$;
(Ⅱ)结论:存在实数m=$\frac{1}{2}$,使得数列{an}是等比数列.
理由如下:
由已知,a1=m,an+1=f(an)=$\frac{{{a}_{n}}^{2}}{1-{a}_{n}}$,
∴a2=$\frac{{m}^{2}}{1-m}$,a3=$\frac{{{a}_{2}}^{2}}{1-{a}_{2}}$,
假设存在实数m,使得数列{an}是等比数列,
则必有${{a}_{2}}^{2}$=a1a3,且an≠0、an≠1,
∴${{a}_{2}}^{2}$=a1•$\frac{{{a}_{2}}^{2}}{1-{a}_{2}}$,即1-a2=a1,1-$\frac{{m}^{2}}{1-m}$=m,解得:m=$\frac{1}{2}$,
当m=$\frac{1}{2}$时,a1=$\frac{1}{2}$,an+1=f(an)=$\frac{1}{2}$,
即数列{an}是等比数列;
(Ⅲ)证明:∵a1=m,0<m<$\frac{1}{2}$,an+1=f(an)=$\frac{{{a}_{n}}^{2}}{1-{a}_{n}}$,
∴an≠0且an+1-anan+1=${{a}_{n}}^{2}$,即an+1=${{a}_{n}}^{2}$+anan+1=an(an+an+1),
∴an+an+1=$\frac{{a}_{n+1}}{{a}_{n}}$,
∴$\underset{\stackrel{n}{π}}{i=1}$(ai+1+ai)=$\frac{{a}_{2}}{{a}_{1}}$•$\frac{{a}_{3}}{{a}_{2}}$•$\frac{{a}_{4}}{{a}_{3}}$•…•$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{{a}_{n+1}}{m}$,
设y=2x2+x-1=2$(x+\frac{1}{4})^{2}$-$\frac{9}{8}$,当0<x<$\frac{1}{2}$时y<0,即0<2x2<1-x,
故当0<x<$\frac{1}{2}$时0<$\frac{{x}^{2}}{1-x}$<$\frac{1}{2}$,
∴当0<m<$\frac{1}{2}$时0<an+1<$\frac{1}{2}$,
∴$\underset{\stackrel{n}{π}}{i=1}$(ai+1+ai)<$\frac{1}{2m}$.
点评 本题是一道关于数列与不等式的综合题,考查数列的通项,考查累乘法,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于难题.


科目:高中数学 来源: 题型:选择题
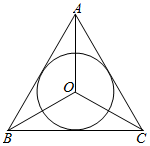 如图:在图O内切于正三角形△ABC,则S△ABC=S△OAB+S△OAC+S△OBC=3•S△OBC,即$\frac{1}{2}•|{BC}|•h=3•\frac{1}{2}•|{BC}|•r$,即h=3r,从而得到结论:“正三角形的高等于它的内切圆的半径的3倍”;类比该结论到正四面体,可得到结论:“正四面体的高等于它的内切球的半径的a倍”,则实数a=( )
如图:在图O内切于正三角形△ABC,则S△ABC=S△OAB+S△OAC+S△OBC=3•S△OBC,即$\frac{1}{2}•|{BC}|•h=3•\frac{1}{2}•|{BC}|•r$,即h=3r,从而得到结论:“正三角形的高等于它的内切圆的半径的3倍”;类比该结论到正四面体,可得到结论:“正四面体的高等于它的内切球的半径的a倍”,则实数a=( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若rn=sn+tn,则{rn}是等比数列 | B. | 若rn=sntn,则{rn}是等比数列 | ||
| C. | 若rn=sn-tn,则{rn}是等比数列 | D. | 以上说明均不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com