
分析 由复合命题P且Q的真假,先判断出简单命题P、Q均为真命题.再依命题P为真命题对a分类讨论确定大致范围,指数不等式求解可采用单调性法.命题Q中,对数函数值域为R可转化为真数能取到(0,+∞)所有值.
解答 ∵P且Q为真命题,∴命题P与命题Q均为真命题.
若a>1,命题P的不等式可转化为x2-ax-2a2>0,解集为:{x|x<-a或x>2a},不合题意.
若0<a<1,命题P成立.此时只需满足命题Q成立即可.
命题Q:函数的值域为R,则真数ax2-x+a能取到所有的正数,即ax2-x+a≤0有解
∴△≥0 即1-4a2≥0解得-$-\frac{1}{2}≤a≤\frac{1}{2}$,又∵0<a<1
所以答案为(0,$\frac{1}{2}$]
点评 考查了复合命题的真假问题,指对数函数的性质.考查函数思想、化归思想.属于中档题


 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a5=b5 | B. | a5>b5 | C. | a5<b5 | D. | 以上都有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 0 | D. | e |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
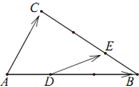 如图,在△ABC中,D、E分别是AB和BC的三等分点,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,则$\overrightarrow{DE}$=( )
如图,在△ABC中,D、E分别是AB和BC的三等分点,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,则$\overrightarrow{DE}$=( )| A. | $\overrightarrow{DE}$=$\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$ | B. | $\overrightarrow{DE}$=$\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$ | C. | $\overrightarrow{DE}$=$\frac{1}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ | D. | $\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com