
分析 由正弦定理可求sinB=$\frac{\sqrt{3}}{2}$,结合范围0<B<π,可得B,从而可求C,由正弦定理即可得解.
解答 解:∵由正弦定理可得:sinB=$\frac{bsinA}{a}$=$\frac{\sqrt{3}×sin\frac{π}{6}}{1}$=$\frac{\sqrt{3}}{2}$,
又∵0<B<π,
∴B=$\frac{π}{3}$或$\frac{2π}{3}$,解得:C=π-A-B=$\frac{π}{2}$或$\frac{π}{6}$.
∴c=$\frac{asinC}{sinA}$=$\frac{1×sinC}{\frac{1}{2}}$=2sinC=2或1.
故答案为:2或1.
点评 本题主要考查了正弦定理的应用,考查了三角形的边角关系的转化,属于基本知识的考查.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1]∪($\frac{1}{2}$,+∞) | B. | (-1,$\frac{1}{2}$] | C. | (-∞,-1)∪[-$\frac{1}{2}$,+∞) | D. | (-1,-$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 一已知函数f(x)=cos(ωx+φ-$\frac{π}{2}$)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则y=f(x+$\frac{π}{6}$)取得最小值时x的集合为( )
一已知函数f(x)=cos(ωx+φ-$\frac{π}{2}$)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则y=f(x+$\frac{π}{6}$)取得最小值时x的集合为( )| A. | {x|x=kπ-$\frac{π}{6}$,k∈z} | B. | {x|x=kπ-$\frac{π}{3}$,k∈z} | C. | {x|x=2kπ-$\frac{π}{6}$,k∈z}} | D. | {x|x=2kπ-$\frac{π}{3}$,k∈z}} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=$\sqrt{5}$r | B. | a=2r | C. | a=$\sqrt{3}$r | D. | a=$\sqrt{2}$r |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G和H分别是CE和CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G和H分别是CE和CF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若-3≤m<n,则f(m)<f(n) | B. | 若m<n≤0,则f(m)<f(n) | ||
| C. | 若f(m)<f(n),则m2<n2 | D. | 若f(m)<f(n),则m3<n3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
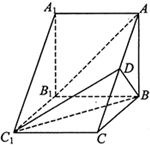 在三棱柱ABC-A1B1C1中,侧棱BB1⊥底面A1B1C1,D为AC 的中点,A1B1=BB1=2,A1C1=BC1,∠A1C1B=60°.
在三棱柱ABC-A1B1C1中,侧棱BB1⊥底面A1B1C1,D为AC 的中点,A1B1=BB1=2,A1C1=BC1,∠A1C1B=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com