Question

4．如图，在多面体ABCDEF中，底面ABCD是边长为2的菱形，∠BAD=60°，四边形BDEF是矩形，平面BDEF⊥平面ABCD，BF=3，G和H分别是CE和CF的中点．
（Ⅰ）求证：平面BDGH∥平面AEF；
（Ⅱ）求CF与平面BDEF所成角的正弦值．

Answer 1

分析 （Ⅰ）根据面面平行的判定定理即可证明平面BDGH∥平面AEF；
（Ⅱ）连接OF，证明OC⊥平面BDEF，即可求CF与平面BDEF所成角的正弦值．

解答 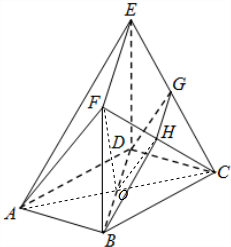（Ⅰ）证明：在△CEF中，因为G，H分别是CE，CF的中点，
所以GH∥EF，
又因为GH?平面AEF，EF?平面AEF，
所以GH∥平面AEF．
设AC∩BD=0，连接OH，
在△ACF中，因为OA=OC，CH=HF，
所以OH∥AF，
又因为OH?平面AEF，AF?平面AEF，
所以OH∥平面AEF．
又因为OH∩GH=H，OH，GH?平面BDGH，
所以平面BDGH∥平面AEF；
（Ⅱ）解：连接OF，则
因为底面ABCD是边长为2的菱形，∠BAD=60°，
所以AC⊥BD，OC=$\sqrt{3}$，BD=1，
因为四边形BDEF是矩形，BF=3，
所以OF=$\sqrt{10}$，
所以CF=$\sqrt{13}$，
因为AC⊥BD，AC⊥FB，FB∩BD=B，
所以OC⊥平面BDEF
所以CF与平面BDEF所成角的正弦值为$\frac{\sqrt{3}}{\sqrt{13}}$=$\frac{\sqrt{39}}{13}$．

点评 本题主要考查线面、面面平行判断，面面垂直的性质，考查线面角，考查学生分析解决问题的能力，要求熟练掌握相应的判定定理．