
分析 (1)根据导数的几何意义解出切点坐标和斜率,带入直线的点斜式方程;
(2)先假设函数是“中值平衡函数”,结合定义得到,通过讨论a的范围,从而确定结论;
(3)使用分离参数法解出a≥$\frac{-{{x}_{0}}^{2}+2{x}_{0}}{ln{x}_{0}-{x}_{0}}$,求后面函数的最小值即可.
解答 解:(1)a=1时,f(x)=lnx+x2-4x,f′(x)=$\frac{1}{x}$+2x-4.
∴f(x)在x=1处的切线斜率k=f′(1)=-1,∵f(1)=-3,
∴f(x)在x=1处的切线方程是y+3=-(x-1),即x+y+2=0.
(2)f′(x)=$\frac{a}{x}$+2x-4,
假设f(x)是中值平衡函数,则存在A(x1,y1),B(x2,y2)(0<x1<x2),使得f′(x0)=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$,
即$\frac{a}{{x}_{0}}$+2x0-4=$\frac{aln{x}_{2}+{{x}_{2}}^{2}-4{x}_{2}-aln{x}_{1}-{{x}_{1}}^{2}+4{x}_{1}}{{x}_{2}-{x}_{1}}$=$\frac{aln\frac{{x}_{2}}{{x}_{1}}}{{x}_{2}-{x}_{1}}$+x2+x1-4.
∵x1+x2=2x0,∴$\frac{2a}{{x}_{1}+{x}_{2}}$=$\frac{aln\frac{{x}_{2}}{{x}_{1}}}{{x}_{2}-{x}_{1}}$,
①当a=0时,上式恒成立,所以函数f(x)是“中值平衡函数”,且函数f(x)的“中值平衡切线”有无数条;
②当a≠0时,令$\frac{{x}_{2}}{{x}_{1}}$=t,则x2=x1t,t>1,∴$\frac{2}{{x}_{1}+{x}_{1}t}$=$\frac{lnt}{{x}_{1}t-{x}_{1}}$,即$\frac{2}{t+1}=\frac{lnt}{t-1}$,∴lnt=$\frac{2t-2}{t+1}=2-\frac{4}{t+1}$.
令h(t)=lnt-2+$\frac{4}{t+1}$,则h′(t)=$\frac{1}{t}$-$\frac{4}{(t+1)^{2}}$=$\frac{(t+1)^{2}-4t}{t(t+1)^{2}}$=$\frac{(t-1)^{2}}{t(t+1)^{2}}$>0,
∴h(t)在(1,+∞)上单调递增,∴h(t)>h(1)=0,
∴h(t)=0无解,即函数f(x)不是“中值平衡函数”.
综上,当a=0时,f(x)是“中值平衡函数”,函数f(x)的“中值平衡切线”有无数条;
当a≠0时,f(x)不是“中值平衡函数”.
(3)∵alnx0+x02-4x0≤(a-2)x0,
∴a(lnx0-x0)≤-x02+2x0.
∵lnx0-x0<0,∴a≥$\frac{-{{x}_{0}}^{2}+2{x}_{0}}{ln{x}_{0}-{x}_{0}}$,
令F(x0)=$\frac{-{{x}_{0}}^{2}+2{x}_{0}}{ln{x}_{0}-{x}_{0}}$,则F′(x0)=$\frac{(2-2{x}_{0})(ln{x}_{0}-{x}_{0})-(2{x}_{0}-{{x}_{0}}^{2})(\frac{1}{{x}_{0}}-1)}{(ln{x}_{0}-{x}_{0})^{2}}$,
∴当$\frac{1}{e}$≤x0<1时,F′(x0)<0,当1<x0≤e时,F′(x0)>0,当x0=1时,F′(x0)=0,
∴F(x0)在[$\frac{1}{e}$,1]上单调递减,在(1,e]上单调递增,
∴Fmin(x0)=F(1)=-1.
∴a的取值范围是[-1,+∞).
点评 本题考查了导数的几何性质,导数在求最值时的应用及对新定义的理解,计算较复杂,属于难题.


科目:高中数学 来源: 题型:解答题
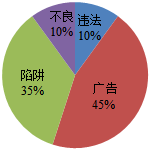 2014年春晚唱响的一曲“群发的我不回”让短信再次成为关注焦点,手机短信中不乏大量垃圾短信,垃圾短信一般分为不良短信、广告短信、违法短信、陷阱短信等四类,其分布如图.
2014年春晚唱响的一曲“群发的我不回”让短信再次成为关注焦点,手机短信中不乏大量垃圾短信,垃圾短信一般分为不良短信、广告短信、违法短信、陷阱短信等四类,其分布如图.| 条数 | [0,5) | [5,10) | [10,15) | [15,20) | [20,25) | [25,30) |
| 人数 | 1 | 2 | 5 | 9 | 5 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com