Question

在正方体ABCD-A₁B₁C₁D₁中，结合各棱长的中点和8个顶点，在这20个点中，任取两点构成的直线中与直线BD₁
垂直的条数是（　　）

• A、18
• B、21
• C、27
• D、36

Answer 1

考点：空间中直线与直线之间的位置关系

专题：空间位置关系与距离

分析：以B为原点，BC，BA，BB₁分别为x，y，z轴建立空间直角坐标系，设正方体棱长为1，BD₁的坐标就是

b

=（1，1，1）把对于各个顶点和各棱的中点（共20个点）组成的集合记为集合E，E中的点坐标形式（x，y，z） 其中x，y，z可以取的值是{0，

1

2

，1}三者中的一个．对x分类讨论，能求出任取两点构成的直线中与直线BD₁
垂直的条数．

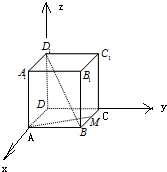
解答： 解：以B为原点，BC，BA，BB₁分别为x，y，z轴建立空间直角坐标系，
设正方体棱长为1
那么BD₁的坐标就是

b

=（1，1，1）
把对于各个顶点和各棱的中点（共20个点）组成的集合记为集合E，
那么E中的点坐标形式（x，y，z） 其中x，y，z可以取的值是{0，

1

2

，1}三者中的一个．
注意到集合E中没有面对角线的交点，也没有正方体的中心，
所以上述（x，y，z）中的分量取值至多只能出现一个

1

2

，
我们把和BD₁垂直的直线对应的向量记为

a

=（x，y，z），
即（x₁-x₂，y₁-y₂，z₁-z₂）
则x，y，z的取值是{0，±

1

2

，±1} 中的一个．
为了避免重复限定x≥0，下面对x分类讨论：
（1）当x=0时，要满足a⊥b，则0+y+z=0≥y+z=0，
此时y，z的取值可以是y=

1

2

，z=-

1

2

，或y=1，z=-1，或y，z取值互换的另两种情况：
①对于y=

1

2

，z=-

1

2

，则对应的直线4条，分别是：
（0，

1

2

，0）-（0，0，

1

2

）
（0，1，

1

2

）-（0，

1

2

，1）
（1，

1

2

，0）-（1，0，

1

2

）
（1，1，

1

2

）-（1，

1

2

，1）
如果y=-

1

2

，z=

1

2

，则上述4条直线中起点和终点交换位置，直线还是同一条，
所以仍然只有4条直线垂直b；
②对于y=1，z=-1 则对应的直线有3条，分别是：
（0，1，0）-（0，0，1）
（

1

2

，1，0）-（

1

2

，0，1）
（1，1，0）-（1，0，1）
同理y和z交换后直线并没有增多，仍然是3条直线垂直b，
综合（1）的情况，x=0时对应的直线有3+4=7条；
（2）当X=

1

2

时，要满足a⊥b，则

1

2

+y+z=0≥y+z=-

1

2

，
此时y，z的取值可以是y=0，z=-

1

2

，或y=

1

2

，z=-1，或y，z取值互换的另两种情况：
①对于y=0，z=-

1

2

，则对应的直线有4条，分别是：
（

1

2

，0，0）-（0，0，

1

2

）
（

1

2

，1，0）-（0，1，

1

2

）
（1，0，

1

2

）-（

1

2

，0，1）
（1，1，

1

2

）-（

1

2

，1，1）
如果y，z互换取值，那么对应的直线又多了4条，
因此这种情况下，对应的直线就有8条；
②对于y=

1

2

，z=-1，则对应的直线有2条，分别是：
（

1

2

，1，0）-（0，

1

2

，1）
（1，

1

2

，0）-（

1

2

，0，1）
同理，如果互换y，z，则对应的直线又多了2条，因此这种情况下，对应的直线就有4条
综合（2）的情况，X=

1

2

时，对应的直线就有8+4=12条；
（3）当x=1时，要满足a⊥b，则1+y+z=0≥y+z=-1，
此时y，z的取值可以是y=0，z=-1，或y=-1，z=0，或y=-

1

2

，z=-

1

2

，
①对于y=0，z=-1 则对应的直线有3条，分别是：
（1，0，0）-（0，0，1）
（1，

1

2

，0）-（0，

1

2

，1）
（1，1，0）-（0，1，1）
②对于y=-1，z=0 情况和①类似，只是交换了y，z的取值而已，因此对应直线也是3条．
③对于y=z=-

1

2

，则对应的直线有2条，分别是
（1，

1

2

，0）-（0，1，

1

2

）
（1，0，

1

2

）-（0，

1

2

，1）
综合（3）的情况，x=1时对应的直线一共有3+3+2=8条．
于是综合（1），（2），（3）和BD₁垂直的直线就有7+12+8=27条．
故选：C．

点评：本题考查正方体ABCD-A₁B₁C₁D₁中，结合各棱长的中点和8个顶点的20个点中，任取两点构成的直线中与直线BD₁垂直的条数的求法，解题时要认真审题，注意分类讨论思想和向量法的合理运用．