考点:导数在最大值、最小值问题中的应用
专题:
分析:(1)令k=1,写出f
1(x)的表达式,再求导,分成a>0,a>0,a=0三种情况讨论,注意到函数的定义域.
(2)由f
2(x)=1,得
=,使问题转化成求函数y=
和y=
的交点个数.考虑函数
g(x)=(x>0),利用求导的方法对其单调性进行研究,同时注意到着g(x)的取值,数形结合求解.
(3)取a=1,k=3时的情况,即
f3(x)=(x>0),利用求导的方法研究其范围,得到不等式
3lnx≤,再结合着e
x>1,即证得不等式成立.
解答:
解:(1)
f1(x)=(x>0),
f′1(x)==(x>0)当a=0时,f′
1(x)=0,f
1(x)无单调区间;
当a≠0时,令f′
1(x)=0,解得x=e.
当a>0时,f
1(x)的单调增区间为(0,e),单减区间为(e,+∞);
当a>0时,f
1(x)的单调增区间为(e,+∞),单减区间为(0,e).
(2)由
=1得:
=.
令
g(x)=(x>0).则
g′(x)==.由g′(x)=0得
x=,
从而g(x)在
(0,)单调递增,在
(,+∞)单调递减.
g(x)max=g()=.
当x→0时,g(x)→-∞;当x→+∞时,g(x)→0.
∴当
0<<,即a>2e时,方程有两个不同解.
当
>,即0<a<2e时,方程有0个解.
当
=,或即a=2e时,方程有唯一解.
综上,当a>2e时,方程有两个不同解.当0<a<2e时,方程有0个解.当a=2e,方程有唯一解.
(3)特别地,当a=1时,由
f3(x)=(x>0)得:
f′3(x)==,
由f′
3(x)=0得
x=e,
则f
3(x)在
(0,e)单调递增,在
(e,+∞)单调递减.
f3(x)max=f3(e)=.
∴
f3(x)=≤,即
3lnx≤.又x>0时,e
x>1.
∴3lnx≤x
3e
x-1.
点评:导数是高考中常考内容,常见的形式有选择题,填空题和解答题,特别是解答题,往往都有一定的难度,需要学生考前多练习,多研究,如第三问中,要观察所证等式的特征,寻找相应的参数值,从而代入计算



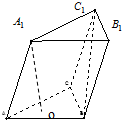 已知三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,A1在底面ABC内的射影O为底面△ABC的中心,如图所示:
已知三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,A1在底面ABC内的射影O为底面△ABC的中心,如图所示: