
分析 (1)利用直线系方程求出直线所过定点,判断定点在圆C内看到直线l与圆C相交;
(2)设P(x,y),由|PD|,|PO|,|PE|成等比数列,得到x2-y2=2,写出$\overrightarrow{PD}$•$\overrightarrow{PE}$=(-2-x,-y)•(2-x,-y)=x2-4+y2=2(y2-1),结合点P在圆C内,得到关于y的不等式,求解不等式得到y的范围,进一步求得$\overrightarrow{PD}$•$\overrightarrow{PE}$的取值范围.
解答 (1)证明:由mx-y+1-m=0,得y=(m-1)x+1,
∴直线l必过定点G(1,1),
又12+(1-1)2<5,∴点G在圆C内部,
∴直线l与圆C相交;
(2)解:设P(x,y),由|PD|,|PO|,|PE|成等比数列,
得$\sqrt{(x+2)^{2}+{y}^{2}}•\sqrt{(x-2)^{2}+{y}^{2}}={x}^{2}+{y}^{2}$,即x2-y2=2,
∴$\overrightarrow{PD}$•$\overrightarrow{PE}$=(-2-x,-y)•(2-x,-y)=x2-4+y2=2(y2-1).
由于点P在圆C内,则$\left\{\begin{array}{l}{{x}^{2}+(y-1)^{2}<5}\\{{x}^{2}-{y}^{2}=2}\end{array}\right.$.
由此得y2-y-1<0,解得:$\frac{1-\sqrt{5}}{2}<y<\frac{1+\sqrt{5}}{2}$.
故$0≤{y}^{2}<(\frac{1+\sqrt{5}}{2})^{2}=\frac{3+\sqrt{5}}{2}$.
∴$2({y}^{2}-1)∈[-2,1+\sqrt{5})$.
∴$\overrightarrow{PD}$•$\overrightarrow{PE}$的取值范围是$[-2,1+\sqrt{5})$.
点评 本题主要考查直线和圆的位置关系的判断,考查向量数量积的坐标运算,考查推理论证能力及运算能力,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{1}{3}$ | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(理)试卷(解析版) 题型:解答题
根据统计资料,某工艺品厂的日产量最多不超过20件根据统计资料,每日产品废品率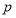 与日产量
与日产量 (件)之间近似地满足关系式
(件)之间近似地满足关系式 (日产品废品率=
(日产品废品率= ×100%) .
×100%) .
已知每生产一件正品可赢利2千元,而生产一件废品则亏损1千元.(该车间的日利润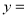 日正品赢利额
日正品赢利额 日废品亏损额)
日废品亏损额)
(1)将该车间日利润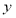 (千元)表示为日产量
(千元)表示为日产量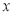 (件)的函数;
(件)的函数;
(2)当该车间的日产量为多少件时,日利润最大?最大日利润是几千元?
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高一上学期月考一数学试卷(解析版) 题型:解答题
已知函数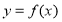 是定义在
是定义在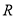 上的奇函数,当
上的奇函数,当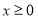 时,
时, .
.
(1)求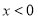 时
时 的解析式;
的解析式;
(2)问是否存在正数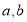 ,当
,当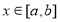 时,
时,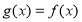 ,且
,且 的值域为
的值域为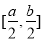 ?若存
?若存
在,求出所有的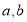 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{9}{4}$,+∞) | B. | [-$\frac{9}{4}$,0] | C. | [-2,0] | D. | [2,4] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com