
分析 (1)令f'(x)>0,得函数f(x)的单调增区间;令f'(x)<0,得函数f(x)的单调减区间;
(2)判断函数的单调性,求出函数的极值以及端点值.由此能求出函数在[-3,4]上的最值.
解答 解:(1)f(x)=x3+2x2-4x+5,
可得f'(x)=3x2+4x-4=(3x-2)(x+2),
令f'(x)=(3x-2)(x+2)>0,
得x<-2或x>$\frac{2}{3}$,
所以函数f(x)的单调增区间为(-∞,-2),($\frac{2}{3}$,+∞);
令f'(x)=(3x-2)(x+2)<0,
得-2<x<$\frac{2}{3}$,
所以函数f(x)的单调减区间为(-2,$\frac{2}{3}$).
(2)x∈[-3,4],因为在[-3-2)上,f'(x)>0,
在(-2,$\frac{2}{3}$)上,f'(x)<0,x∈($\frac{2}{3}$,4],f'(x)>0;
所以f(x)在(-2,$\frac{2}{3}$)单调递减,x∈[-3-2),x∈($\frac{2}{3}$,4],函数是增函数,
f(-3)=8,f(-2)=13,f($\frac{2}{3}$)=$\frac{95}{27}$,f(4)=85
所以x=$\frac{2}{3}$时,[f(x)]min=f($\frac{2}{3}$)=$\frac{95}{27}$.
当x=4时,[f(x)]max=85.
点评 本题考查函数的单调区间和函数的最值的求法,解题时要认真审题,仔细解答,注意导数的性质的灵活运用.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0.5 | C. | 2 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2ab-1-a2b2≥0 | B. | (a2-1)(b2-1)≥0 | ||
| C. | $\frac{(a+b)2}{2}$-1-a2b2≥0 | D. | a2+b2-1-$\frac{{a}^{4}+{b}^{4}}{2}$≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 2 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
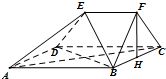 如图,在多面体ABCDEF中,四边形ABCD是正方形,H为BC中点,且FH⊥平面ABCD,EF∥AB,∠BFC=90°,AB=2,EF=1.
如图,在多面体ABCDEF中,四边形ABCD是正方形,H为BC中点,且FH⊥平面ABCD,EF∥AB,∠BFC=90°,AB=2,EF=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com