
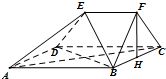
 如图,在多面体ABCDEF中,四边形ABCD是正方形,H为BC中点,且FH⊥平面ABCD,EF∥AB,∠BFC=90°,AB=2,EF=1.
如图,在多面体ABCDEF中,四边形ABCD是正方形,H为BC中点,且FH⊥平面ABCD,EF∥AB,∠BFC=90°,AB=2,EF=1.分析 (Ⅰ)设AC与BD交于G,则G为AC的中点.连接EG,GH,通过证明四边形EFHG是平行四边形,证明FH∥平面EDB;
(Ⅱ)在平面CDEF内过点F作FK⊥DE交DE的延长线与k,可知∠FKB为二面角B-DE-C的一个平面角,然后设EF=1,在直角三角形中进行求解;
(Ⅲ)求出四面体B-DEF的高与底面面积,即可求解四面体的体积.
解答 (Ⅰ)证明:设AC与BD交于G,则G为AC的中点.连接EG,GH,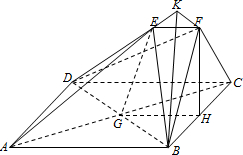
由于H为BC的中点,故GH∥$\frac{1}{2}$AB,GH=$\frac{1}{2}AB$,
又EF$∥\frac{1}{2}$AB,EF=$\frac{1}{2}AB$,
∴四边形EFGH为平行四边形,
∴FH∥平面EDB;
(Ⅱ)解:∵FH⊥平面ABCD,∴平面BFC⊥平面ABCD,
又AB⊥BC,∴AB⊥平面BFC,则AB⊥BF,则EF⊥FB,
又∠BFC=90°,∴BF⊥平面CDEF,
在平面CDEF内过点F作FK⊥DE交DE的延长线与k,则
∠FKB为二面角B-DE-C的一个平面角,
∵EF=1,AB=2,∴FC=$\sqrt{2}$,DE=$\sqrt{3}$,
又EF∥DC,∴∠KEF=∠EDC,
∴sin∠EDC=sin∠KEF=$\frac{\sqrt{2}}{\sqrt{3}}$,
∴FK=EFsin∠KEF=$\frac{\sqrt{2}}{\sqrt{3}}$,
tan∠FKB=$\frac{BF}{FK}$=$\sqrt{3}$,
∴∠FKB=60°,
∴二面角B-DE-C为60°;
(Ⅲ)解:∵EF⊥FB,∠BFC=90°,∴BF⊥平面CDEF,
∴BF为四面体B-DEF的高,
又BC=AB=2,∴BF=FC=$\sqrt{2}$,S=$\frac{1}{2}$EF•FC=$\frac{1}{2}$×1×$\sqrt{2}$,
四面体B-DEF的体积.VB-DEF=$\frac{1}{3}×\frac{1}{2}×1×\sqrt{2}×\sqrt{2}$=$\frac{1}{3}$.
点评 本题考查直线与平面平行的判定定理,直线与平面垂直的判定定理,几何体的体积的求法,考查计算能力,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 44 J | B. | 46 J | C. | 48 J | D. | 50 J |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
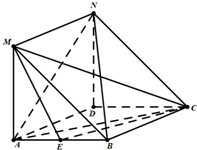 如图,在菱形ABCD中,∠DAB=60°,E是AB的中点,MA⊥平面ABCD,且在矩形ADNM中,AD=2,AM=3.
如图,在菱形ABCD中,∠DAB=60°,E是AB的中点,MA⊥平面ABCD,且在矩形ADNM中,AD=2,AM=3.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com