
(本题满分14分)为改善购物环境,提高经济效益,某商场决定投资800万元改造商场内部环境,据调查,改造好购物环境后,任何一个月内(每月按30天计算)每天的顾客人数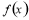 与第x天近似地满足
与第x天近似地满足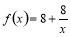 (千人),且每位顾客人均购物金额数
(千人),且每位顾客人均购物金额数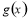 近似地满足
近似地满足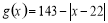 (元).
(元).
(1)求该商场第x天的销售收入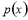 (单位千元,1≤x≤30,
(单位千元,1≤x≤30,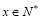 )的函数关系;
)的函数关系;
(2)若以最低日收入的20%作为每一天纯收入的计量依据,商场决定以每日纯收入的5%收回投资成本,试问商场在两年内能否收回全部投资成本.
(1) =
= ;
;
(2)该商场在两年内能收回全部投资成本.
【解析】
试题分析:(1)由题意p(x)=f(x)g(x),代入化简即可;
(2)由分段函数可知,要分段求函数的最小值,从而求出函数的最小值,转化为实际问题即可.
试题解析:(1)依题意有p(x)=f(x)•g(x)
=(8+ )(143-|x-22|)(1≤x≤30,x∈N*)
)(143-|x-22|)(1≤x≤30,x∈N*)
= ;
;
(2)①当1≤x≤22,x∈N*时,
p(x)=8x+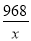 +976≥2
+976≥2 +976=1152(当且仅当x=11时,等号成立)
+976=1152(当且仅当x=11时,等号成立)
∴p(x)min=p(11)=1152(千元),
②当22<x≤30,x∈N*时,p(x)=-8x+ +1312,考察函数y=-8x+
+1312,考察函数y=-8x+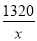 ,
,
可知函数y=-8x+ 在(22,30]上单调递减,
在(22,30]上单调递减,
∴p(x)min=p(30)=1116(千元),
又1152>1116,∴日最低收入为1116千元.
该商场两年可收回的投资资金为:
1116×20%×5%×30×12×2=8035.2(千元)=803.52(万元).
∵803.52>800 ∴该商场在两年内能收回全部投资成本.
考点:函数最值的应用.


科目:高中数学 来源:2015届湖北省咸宁市高三三校联考文科数学试卷(解析版) 题型:填空题
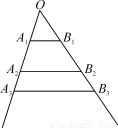
如图,互不相同的点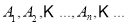 和
和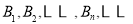 分别在角O的两条边上,所有
分别在角O的两条边上,所有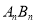 相互平行,且所有梯形
相互平行,且所有梯形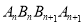 的面积均相等.设
的面积均相等.设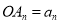 ,若
,若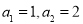 ,则
,则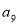 =________________;
=________________;
查看答案和解析>>
科目:高中数学 来源:2015届湖北省八校高三第一次联考理科数学试卷(解析版) 题型:填空题
以(0, m)间的整数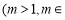 N)为分子,以m为分母组成分数集合A1,其所有元素和为a1;以
N)为分子,以m为分母组成分数集合A1,其所有元素和为a1;以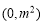 间的整数
间的整数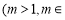 N)为分子,以
N)为分子,以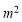 为分母组成不属于集合A1的分数集合A2,其所有元素和为a2; ,依次类推以
为分母组成不属于集合A1的分数集合A2,其所有元素和为a2; ,依次类推以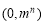 间的整数
间的整数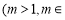 N)为分子,以
N)为分子,以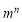 为分母组成不属于A1,A2, ,
为分母组成不属于A1,A2, ,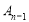 的分数集合An,其所有元素和为an;则
的分数集合An,其所有元素和为an;则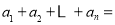 =________.
=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com