练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设函数f(x)＝ax＋sinx＋cosx．若函数f(x)的图象上存在不同的两点A，B，使得曲线y＝f(x)在点A，B处的切线互相垂直，则实数a的取值范围为      ．


    [-1,1]

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知f(x)＝32x－(k＋1)3x＋2，当x∈R时，f(x)恒为正值，则k的取值范围是(　　)

    A．(－∞，－1)                    B．(－∞，2－1)

    C．(－1,2－1)                 D．(－2－1,2－1)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列函数中，为偶函数且有最小值的是(　　)

    A．f(x)＝x2＋x                  B．f(x)＝|ln x|

    C．f(x)＝xsin x                 D．f(x)＝ex＋e－x

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知复数z1＝－2＋i，z2＝a＋2i(i为虚数单位，aR)．若z1z2为实数，则a的值为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    表面积为12π的圆柱，当其体积最大时，该圆柱的底面半径与高的比为      ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝ex，a，b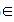R，且a＞0．

    （1）若a＝2，b＝1，求函数f(x)的极值；

    （2）设g(x)＝a(x－1)ex－f(x)．

    ① 当a＝1时，对任意x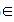 (0，＋∞)，都有g(x)≥1成立，求b的最大值；

    ② 设g′(x)为g(x)的导函数．若存在x＞1，使g(x)＋g′(x)＝0成立，求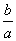的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     设f(n)是定义在N*上的增函数，f(4)＝5，且满足：

    ①任意n∈N*，f(n) 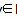Z；②任意m，n∈N*，有f(m)f(n)＝f(mn)＋f(m＋n－1)．

    （1）求f(1)，f(2)，f(3)的值；（2）求f(n)的表达式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     已知全集U＝R，集合M＝{x|－2≤x－1≤2}和N＝{x|x＝2k－1，k＝1，2，…}的韦恩(Venn)图如图所示，则阴影部分所示的集合的元素共有________个．

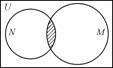
    查看答案和解析>>

    科目：高中数学 来源： 题型：


     设α、β为两个不同的平面，直线lα，则“l⊥β”是“α⊥β”成立的________条件．

    查看答案和解析>>

    同步练习册答案