
 为正方形,四边形
为正方形,四边形 为等腰梯形,
为等腰梯形, ,
, ,
, ,
, .
.
 平面
平面 ;
; 的体积;
的体积; 上是否存在点
上是否存在点 ,使
,使 平面
平面 ?请证明你的结论.
?请证明你的结论.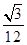 ;(3)详见解析.
;(3)详见解析.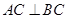 ,再结合
,再结合 并利用直线与平面垂直的判定定理证明
并利用直线与平面垂直的判定定理证明 平面
平面 ;(2)先证明
;(2)先证明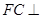 平面
平面 ,从而得到
,从而得到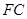 为三棱锥
为三棱锥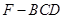 的高,并计算
的高,并计算 的面积作为三棱锥
的面积作为三棱锥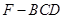 的底面积。最后利用锥体的体积公式计算四面体
的底面积。最后利用锥体的体积公式计算四面体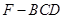 的体积;(3)连接
的体积;(3)连接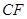 交
交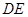 于点
于点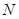 ,根据平行四边形的性质得到
,根据平行四边形的性质得到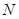 为
为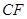 的中点,然后取
的中点,然后取 的中点
的中点 ,构造
,构造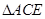 底边的中位线
底边的中位线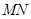 ,得到
,得到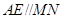 ,结合直线与平面平行的判定定理得到
,结合直线与平面平行的判定定理得到 平面
平面 .
. 中,因为
中,因为 ,
,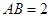 ,
,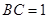 ,
,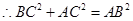 ,
,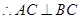 ,
, ,且
,且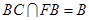 ,
,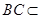 平面
平面 ,
,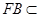 平面
平面 ,
,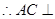 平面
平面 ;
; 平面
平面 ,且
,且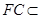 平面
平面 ,
,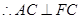 ,
,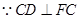 ,且
,且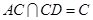 ,
,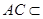 平面
平面 ,
,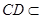 平面
平面 ,
,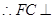 平面
平面 ,即
,即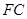 为三棱锥
为三棱锥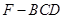 的高,
的高, 中可得
中可得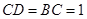 ,所以
,所以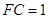 ,
, 的面积为
的面积为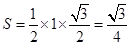 ,
, 的体积为
的体积为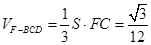 ;
; 上存在点
上存在点 ,且
,且 为
为 的中点时,有
的中点时,有 平面
平面 ,
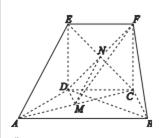
,
 ,
, 与
与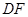 交于点
交于点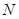 ,连接
,连接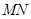 ,
,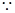 四边形
四边形 为正方形,所以
为正方形,所以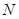 为
为 的中点,
的中点, 为
为 的中点,
的中点,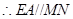 ,
,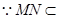 平面
平面 ,
,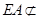 平面
平面 ,
,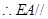 平面
平面 ,
, 上存在点
上存在点 ,使得
,使得 平面
平面 成立.
成立.

 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源:不详 题型:解答题

 ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 AC
AC B的大小为60°.过P作PH⊥EF于H.
B的大小为60°.过P作PH⊥EF于H.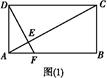
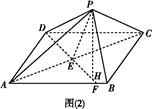
 ABC体积的最大值.
ABC体积的最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com